Simulado UFF de Matematica | VESTIBULAR
SIMULADO UFF DE MATEMATICA
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores Vestibular do País, através de simulados para Vestibular, provas e questões de Vestibular.
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no Vestibular UFF.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da UFF que foi organizado pela UFF . Estas questões são de Matematica, contendo os assuntos de Álgebra , Potência, Matrizes , Álgebra Linear, Aritmética e Problemas , Estatística , Médias, Estatística, Função Exponencial, Geometria Espacial , Esfera, Frações e Números Decimais, Razão e Proporção; e Números Proporcionais, Porcentagem, Números Complexos, Sistema de Unidade de Medidas, Raciocínio Lógico , Sistemas de Numeração e Operações Fundamentais, Geometria Espacial , Cilindro, ( assuntos), Trigonometria, Sistemas Lineares , Álgebra Linear, Função Exponencial que foram extraídas dos Vestibular anteriores UFF, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Simulado UFF de Matematica contém um total de 17 questões de Vestibular com um tempo estimado de 51 minutos para sua realização. Os assuntos abordados são de Matematica, Álgebra , Potência, Matrizes , Álgebra Linear, Aritmética e Problemas , Estatística , Médias, Estatística, Função Exponencial, Geometria Espacial , Esfera, Frações e Números Decimais, Razão e Proporção; e Números Proporcionais, Porcentagem, Números Complexos, Sistema de Unidade de Medidas, Raciocínio Lógico , Sistemas de Numeração e Operações Fundamentais, Geometria Espacial , Cilindro, ( assuntos), Trigonometria, Sistemas Lineares , Álgebra Linear, Função Exponencial para que você possa realmente simular como estão seus conhecimento no Vestibular UFF.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no Vestibular UFF. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Vestibular. Se você esta estudando para ser aprovado para Vestibular não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO UFF
Para realizar o simulado UFF você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado UFF você verá as questões que errou e acertou.
Bons Estudos! Simulado para UFF é aqui!
- #120593
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
Muitos consideram a Internet como um novo continente que transpassa fronteiras geográficas e conecta computadores dos diversos países do globo. Atualmente, para que as informações migrem de um computador para outro, um sistema de endereçamento denominado IPv4 (Internet Protocol Version 4) é usado. Nesse sistema, cada endereço é constituído por quatro campos, separados por pontos. Cada campo, por sua vez, é um número inteiro no intervalo [0, 28 - 1]. Por exemplo, o endereço IPv4 do servidor WEB da UFF é 200.20.0.21. Um novo sistema está sendo proposto: o IPv6. Nessa nova versão, cada endereço é constituído por oito campos e cada campo é um número inteiro no intervalo [0, 216 - 1].
Com base nessas informações, é correto afirmar que
- a) o número de endereços diferentes no sistema IPv6 é o quádruplo do número de endereços diferentes do sistema IPv4.
- b) existem exatamente 4. (28 - 1) endereços diferentes no sistema IPv4.
- c) existem exatamente 232 endereços diferentes no sistema IPv4.
- d) o número de endereços diferentes no sistema IPv6 é o dobro do número de endereços diferentes do sistema IPv4.
- e) existem exatamente (28 - 1) 4 endereços diferentes no sistema IPv4.
- #120594
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
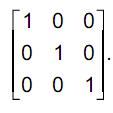
A transmissão de mensagens codificadas em tempos de conflitos militares é crucial. Um dos métodos de criptografia mais antigos consiste em permutar os símbolos das mensagens. Se os símbolos são números, uma permutação pode ser efetuada usando-se multiplicações por matrizes de permutação, que são matrizes quadradas que satisfazem as seguintes condições:
· cada coluna possui um único elemento igual a 1 (um) e todos os demais elementos são iguais a zero;
· cada linha possui um único elemento igual a 1 (um) e todos os demais elementos são iguais a zero.
Por exemplo, a matriz M =

permuta os elementos da matriz coluna Q =

, transformando-a na matriz P =

pois P = M . Q .
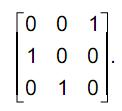
Pode-se afirmar que a matriz que permuta

, transformando-a em

, é
- a)
- b)
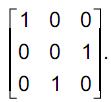
- c)
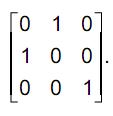
- d)

- e)
- #120595
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
O índice de Theil, um indicador usado para medir desigualdades econômicas de uma população, é definido por

sendo

respectivamente, as médias aritmética e geométrica das rendas X1, X2, ..., XN (consideradas todas positivas e medidas com uma mesma unidade monetária) de cada um dos N indivíduos da população.
Com base nessas informações, assinale a afirmativa incorreta.
- a)
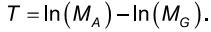
- b)

- c)

- d)
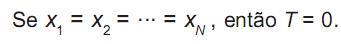
- e)
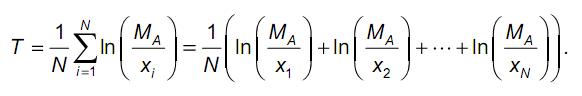
- #120596
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Diz-se que uma família vive na pobreza extrema se sua renda mensal por pessoa é de, no máximo, 25% do salário mínimo nacional. Segundo levantamento do Instituto de Pesquisa Econômica Aplicada (Ipea), mais de treze milhões de brasileiros saíram da pobreza extrema entre 1995 e 2008. No entanto, a diminuição generalizada nas taxas de pobreza extrema nesse período não ocorreu de forma uniforme entre as grandes regiões geográficas do país, conforme ilustra o gráfico abaixo.
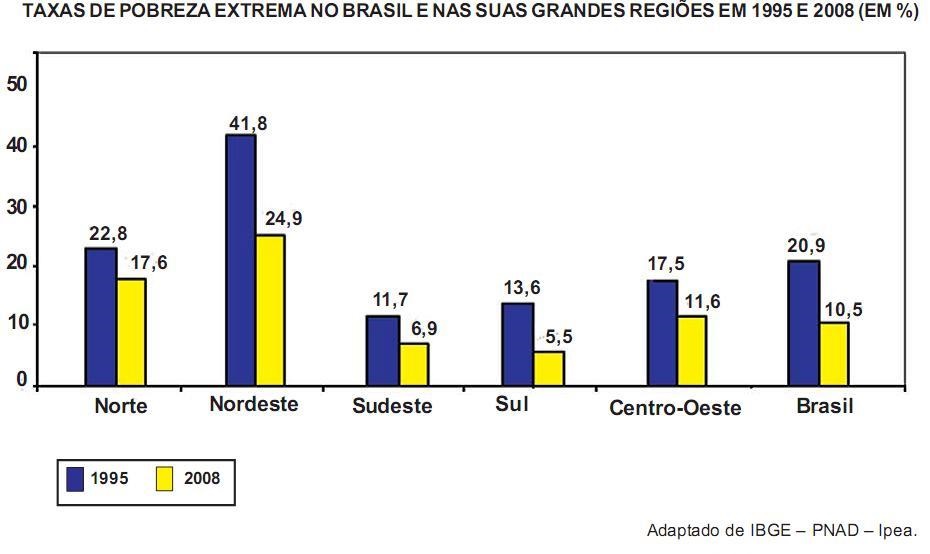
Tendo em vista o gráfico, verifica-se que a taxa nacional de pobreza extrema caiu 49,8%, passando de 20,9% para 10,5%. Pode-se concluir, então, que a região em que a taxa de pobreza extrema (em %) caiu mais de 50% foi
- a) a região Norte.
- b) a região Sudeste.
- c) a região Nordeste.
- d) a região Centro-Oeste.
- e) a região Sul.
- #120597
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Os gráficos I, II e III, abaixo, esboçados em uma mesma escala, ilustram modelos teóricos que descrevem a população de três espécies de pássaros ao longo do tempo.
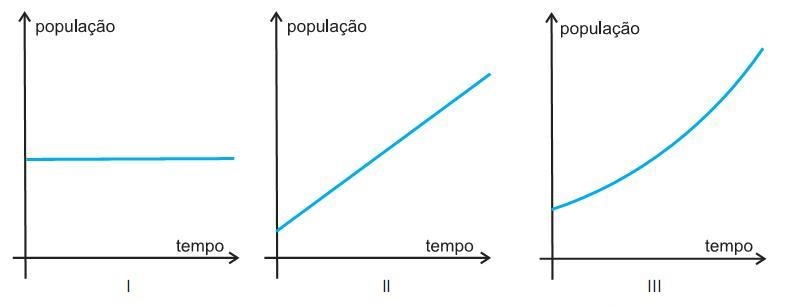
Sabe-se que a população da espécie A aumenta 20% ao ano, que a população da espécie B aumenta 100 pássaros ao ano e que a população da espécie C permanece estável ao longo dos anos.
Assim, a evolução das populações das espécies A, B e C, ao longo do tempo, correspondem, respectivamente, aos gráficos
- a) I, III e II.
- b) II, I e III.
- c) II, III e I.
- d) III, I e II.
- e) III, II e I.
- #120598
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
Para ser aprovada pela FIFA, uma bola de futebol deve passar por vários testes. Um deles visa garantir a esfericidade da bola: o seu “diâmetro” é medido em dezesseis pontos diferentes e, então, a média aritmética desses valores é calculada. Para passar nesse teste, a variação de cada uma das dezesseis medidas do “diâmetro” da bola com relação à média deve ser no máximo 1,5%. Nesse teste, as variações medidas na Jabulani, bola oficial da Copa do Mundo de 2010, não ultrapassaram 1%.
Se o diâmetro de uma bola tem aumento de 1%, então o seu volume aumenta x %.

Dessa forma, é correto afirmar que
- a) x ∈ [5,6).
- b) x ∈ [2,3)
- c) x = 1.
- d) x ∈ [3,4).
- e) x ∈ [4,5).
- #120599
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
Ao se fazer um exame histórico da presença africana no desenvolvimento do pensamento matemático, os indícios e os vestígios nos remetem à matemática egípcia, sendo o papiro de Rhind um dos documentos que resgatam essa história.
Nesse papiro encontramos o seguinte problema:
“Divida 100 pães entre 5 homens de modo que as partes recebidas estejam em progressão aritmética e que um sétimo da soma das três partes maiores seja igual à soma das duas menores.”

Coube ao homem que recebeu a parte maior da divisão acima a quantidade de
- a) 115 pães3
- b) 55 pães6
- c) 20 pães.
- d) 65 pães6
- e) 35 pães.
- #120600
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Como mostram vários censos, nossa civilização habita o globo terrestre de maneira muito desigual. A densidade demográfica de uma região é a razão entre o número de seus habitantes e a sua área. Através desse índice, é possível estudar a ocupação de um território por uma determinada população.
Com relação à densidade demográfica, assinale a afirmativa incorreta.
- a) Se o número de habitantes de uma região dobra e sua área permanece a mesma, então a densidade demográfica dessa região também dobra.
- b) Se duas regiões possuem o mesmo número de habitantes, então a região com maior área possui uma densidade demográfica maior.
- c) Se duas regiões possuem a mesma área, então a região com maior número de habitantes possui uma densidade demográfica maior.
- d) Se duas regiões possuem a mesma área e o mesmo número de habitantes, então elas possuem a mesma densidade demográfica.
- e) Se uma região tem 150 000 000 de habitantes e área igual a 7 500 000 km2 , então sua densidade demográfica é igual a 20 habitantes/km2 .
- #120601
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
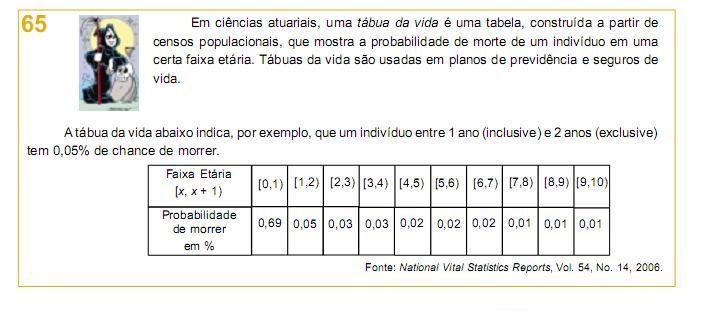
Supondo-se que existe um grupo de 1 000 000 pessoas que acabaram de completar 2 anos, segundo esta tabela, o número de pessoas deste grupo que farão aniversário de 3 anos é igual a:
- a) 997 000
- b) 999 500
- c) 999 700
- d) 999 950
- e) 999 970
- #120602
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -

Dentre as alternativas a seguir, assinale aquela que indica uma afirmação incorreta.
- a) o conjugado de (1 + i) é (1- i)
- b) |1 + i| =√2
- c) (1 + i) é raiz da equação z 2 -2z + 2 = 0
- d) (1 + i) -1 = (1- i)
- e) (1 + i) 2 = 2i
- #120603
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 11 -

Admitindo-se que um DVD comum é capaz de armazenar 4 gigabytes (na verdade, ele armazena um pouco mais), então o número de DVDs necessários para se armazenar 3 petabytes é:
- a) menor que 217 e maior que 216
- b) maior que 2 20
- c) menor que 219 e maior que 218
- d) menor que 218 e maior que 217
- e) menor que 220 e maior que 2 19
- #120604
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 12 -

Sabendo que o ano de 1600 é bissexto, pode-se afirmar que entre 1601 e 2007 ocorreram:
- a) 97 anos bissextos
- b) 98 anos bissextos
- c) 99 anos bissextos
- d) 100 anos bissextos
- e) 101 anos bissextos
- #120605
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 13 -
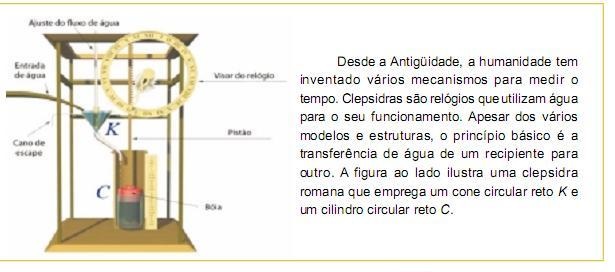
Sabendo-se que K e C possuem bases circulares congruentes e que o volume de C é dez vezes o volume de K, pode-se afirmar que a razão entre a altura do cilindro e a altura do cone é igual a:
- a) 10⁄7
- b) 10
- c) 3
- d) 10⁄3
- e) 1⁄3
- #120606
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 14 -
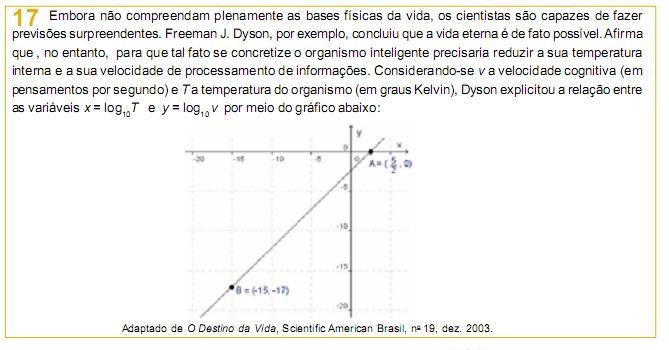
Sabendo-se que o gráfico da figura está contido em uma reta que passa pelos pontos A = ( 5⁄2 , 0)e B = ( - 15, -17), assinale a alternativa que contém a equação que descreve a relação entre x e y.
- a) y = 34 ⁄35 x - 17⁄ 7
- b) y = x - 5⁄ 2
- c) y = 34 ⁄30 x - 17 5
- d) y = 5⁄ 2 x - 17⁄ 5
- e) y = 34⁄ 35 x + 5⁄ 2
- #120607
- Banca
- UFF
- Matéria
- Matemática
- Concurso
- UFF
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 15 -

É correto afirmar que:
- a) f(B) = 9,87 sen(2 B) – 7,53 cos(B) – 0,75 sen(2 B)
- b) f(B) = 19,74 sen(B) – 7,53 cos(B) – 1,5 sen(B)
- c) f(B) = [19,74 sen(B) – 7,53] cos(B) – 1,5 sen(B)
- d) f(B) = 9,87 [2 (cos(B))2 – 1] – 1,5 sen(B) – 7,53 cos(B)
- e) f(B) = 8,37 sen(2 B) – 7,53 cos(B)

