Simulado TRT 6° REGIÃO | Analista Judiciário – Estatística | CONCURSO

(1,0) 1 - 

A probabilidade de que no quinto lançamento de um dado não viciado (numerado de 1 a 6) ocorra a face 3 pela segunda vez é

(1,0) 2 - 

As probabilidades de um contador, A, demorar uma, duas ou três horas para preencher uma declaração de imposto de renda são dadas, respectivamente, por ¹/₄, ¹/₂ e ¹/₄ . Dentre 5 declarações escolhidas aleatoriamente e com reposição, das declarações que A deverá elaborar, a probabilidade dele demorar para o preenchimento, em três delas 1 hora, em uma 2 horas e na restante 3 horas, é igual a

(1,0) 3 - 

De 30 caminhões de entrega de encomendas de uma grande loja de departamentos, 6 emitem excesso de poluentes. Selecionam-se aleatoriamente e sem reposição uma amostra de n caminhões para a inspeção de poluentes. Seja X a variável aleatória que representa o número de caminhões com excesso de poluentes na amostra. Sabendo-se que a média de X é 2,4, o valor de n é

(1,0) 4 - 

A caixa A tem 5 cartas numeradas de 1 a 5. A caixa B tem 8 cartas numeradas de 1 a 8. A caixa C tem 10 cartas numeradas de 1 a 10. Uma caixa é selecionada ao acaso e uma carta é retirada. Se o número da carta é impar, a probabilidade de a carta selecionada ter vindo da caixa B é

(1,0) 5 - 

Um experimento consiste de tentativas independentes de um mesmo experimento aleatório de Bernoulli. Em cada tentativa a probabilidade de fracasso é igual a ³/₄ da probabilidade de sucesso. Seja X a variável aleatória que representa o número de tentativas até o aparecimento do primeiro sucesso. A variância de X é igual a

(1,0) 6 - 

Seja o modelo linear de análise de covariância

referente a um determinado ramo de atividade.

representa o salário anual de um empregado

é o número de anos de experiência do empregado i e ei é o erro aleatório com as respectivas hipóteses da correspondente regressão (a, ß e γ são parâmetros desconhecidos). Com relação a este modelo, dado que

se o empregado i for homem e

se o empregado i for mulher, pode-se afirmar que

(1,0) 7 - 

Todos os funcionários de 5 grupos de trabalho com 6 funcionários cada um, escolhidos aleatoriamente, são designados para realizar uma tarefa, independentemente. O tempo que cada um dos 30 funcionários levou para concluir a tarefa é anotado. Deseja-se saber, a um determinado nível de significância, se os tempos médios dos grupos para a realização da tarefa são iguais. Considere algumas informações do quadro de análise de variância:

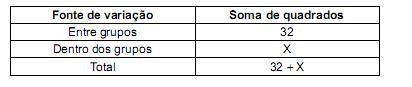
Se o valor da estatística F (F calculado) utilizado para testar a igualdade dos tempos médios apresentou um valor igual a 20, então X é igual a

(1,0) 8 - 

Seja o modelo de regressão linear múltipla

de uma certa população, em que:

I.

é variável dependente,

II.

são as variáveis explicativas,

III. a, ß e γ são parâmetros desconhecidos,

IV.

o erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla,

V. i é a i-ésima observação,

VI. n é o número de observações.

Considere que n = 20 e que as estimativas de a, ß e γ foram obtidas pelo método dos mínimos quadrados. O valor da estatística F (F calculado) utilizado para testar a existência da regressão, a um determinado nível de significância apresentou um valor igual a 31,5. O poder de explicação deste modelo (R²), definido como sendo o resultado da divisão da respectiva variação explicada pela variação total, é igual a

(1,0) 9 - 

Em 3 cidades X, Y e Z foram escolhidos aleatoriamente, em cada uma, 50 consumidores de um produto. Deseja-se saber, ao nível de significância de 5%, se o nível de satisfação do produto depende da cidade onde ele é consumido. Em cada cidade foi perguntado, independentemente, para cada consumidor quanto à satisfação do produto. O resultado pode ser visualizado pela tabela abaixo.

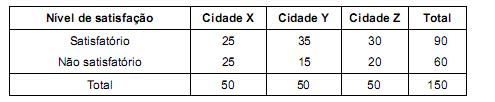
Utilizou-se o teste qui-quadrado para analisar se existe dependência do nível de satisfação com relação às cidades.

Dados: Valores críticos da distribuição qui-quadrado P[(qui-quadrado com n graus de liberdade < valor tabelado) = 95%].

O valor do qui-quadrado observado e a conclusão se o nível de satisfação depende da cidade, ao nível de significância de 5%, é

(1,0) 10 - 

Em uma grande empresa, n empregados, escolhidos aleatoriamente, são submetidos a um teste que mede o conhecimento da língua inglesa. Decide-se dar um curso de inglês para estes funcionários, durante um ano. Após este período, todos são submetidos a um novo teste, notando-se que 62,5% dos empregados apresentaram melhora e os restantes foram melhores no primeiro teste. Para decidir se o curso funcionou, a um nível de significância a, utilizou-se o teste dos sinais, atribuindo sinais positivos para os empregados que apresentaram melhora e sinais negativos para os que foram melhores no primeiro teste. Seja p a proporção populacional de sinais positivos e as hipóteses

(hipótese nula) e

(hipótese alternativa). O valor do escore reduzido, sem a correção de continuidade, utilizado para comparação com o valor crítico z da distribuição normal padrão (Z), tal que a probabilidade P(Z > z) = a, é igual a 2,0. O valor de n é igual a

(1,0) 11 - 

O tamanho de uma população normalmente distribuída, com um desvio padrão populacional igual a 128, é igual a 1025. Uma amostra aleatória de tamanho 64 é extraída, sem reposição, desta população. Com base nesta amostra e considerando que na distribuição normal padrão (Z) a probabilidade P(Z > 1,96) = 0,025, obteve-se um intervalo de confiança de 95% com uma amplitude igual a

(1,0) 12 - 

Uma variável aleatória X é normalmente distribuída com média µ, variância populacional igual a 576 e com uma população considerada de tamanho infinito. Por meio de uma amostra aleatória de tamanho 100, obteve-se um intervalo de confiança de (1 - a) para µ igual a [105,8 ; 114,2]. Uma outra amostra aleatória de tamanho 225, independente da primeira, forneceu uma média amostral igual a 108. Então, o intervalo de confiança de (1 - a) correspondente a esta outra amostra é igual a

(1,0) 13 - 

Deseja-se obter uma estimativa pontual do parâmetro p da distribuição geométrica P(X = x) = (1 - p) ^{x - 1} p (x = 1, 2, 3, . . . ) sabendo-se que o acontecimento cuja probabilidade é p ocorreu em 5 experiências, pela primeira vez na primeira, terceira, segunda, quarta e segunda, respectivamente. Utilizando o método dos momentos, encontra-se que o valor desta estimativa é

(1,0) 14 - 

Em um conjunto de 100 experiências, consistindo em 5 provas cada uma, verificou-se se o evento A ocorre em cada prova. Seja a distribuição abaixo referente a estas experiências:

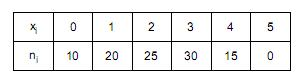
Observação:

é o número de experiências nas quais o evento A ocorreu

vezes.

Admitindo que a ocorrência do evento A em cada experiência obedece a uma distribuição binomial, ou seja,

encontra-se, pelo método da máxima verossimilhança, que uma estimativa pontual do parâmetro p é

(1,0) 15 - 

Considere uma amostra aleatória (X, Y, Z), com reposição, extraída de uma população normal com média µ e variância 1. Considere também os 3 estimadores não viesados de µ , com m, n e p sendo parâmetros reais:

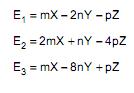
Entre os 3 estimadores, o mais eficiente apresenta uma variância igual a