Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística | CONCURSO

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 1

   ×

   Para resolver à questão use, das informações dadas a seguir, as que julgar apropriadas.Se Z tem distribuição normal padrão, então:P(Z < 0,4) = 0,655; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885 P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2,0) = 0,977; P(Z < 2,4) = 0,997Seja

   

   uma variável aleatória normal bivariada com vetor de médias

   

   e matriz de covariâncias

   

   Fechar

(1,0) 1 - 

Suponha que μ_x = 4 e que 25 σ_y²= . Nessas condições, a probabilidade expressa por P(14 < U < 25), onde U é a variável aleatória definida por U = aZ, com a = [2, −1], é igual a

(1,0) 2 - 

Sabendo que a probabilidade de Y assumir um valor entre 1 e 5 é igual a 0,477, o valor de σ_y²é igual a

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 1

   ×

   Para resolver à questão use, das informações dadas a seguir, as que julgar apropriadas.Se Z tem distribuição normal padrão, então:P(Z < 0,4) = 0,655; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885 P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2,0) = 0,977; P(Z < 2,4) = 0,997Seja

   

   uma variável aleatória normal bivariada com vetor de médias

   

   e matriz de covariâncias

   

   Fechar

(1,0) 3 - 

Sabendo que a probabilidade da variável aleatória X assumir um valor inferior a 2 é igual a 0,115, o valor de μ_x é igual a

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 1

   ×

   Para resolver à questão use, das informações dadas a seguir, as que julgar apropriadas.Se Z tem distribuição normal padrão, então:P(Z < 0,4) = 0,655; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885 P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2,0) = 0,977; P(Z < 2,4) = 0,997Seja

   

   uma variável aleatória normal bivariada com vetor de médias

   

   e matriz de covariâncias

   

   Fechar

(1,0) 4 - 

Considere as seguintes afirmações relativas à Análise Multivariada:
I. A análise de Correlação canônica é considerada uma técnica de interdependência, isto é, nessa análise as variáveis em questão não podem ser consideradas como dependentes ou independentes. II. O propósito básico da análise discriminante é estimar a relação entre uma variável dependente categórica com base em um conjunto de variáveis independentes métricas. III. A análise de agrupamentos é uma técnica analítica cujo objetivo é classificar uma amostra de entidades (indivíduos ou objetos) em um número menor de grupos mutuamente excludentes, com base nas similaridades entre as entidades. IV. A análise de correspondência usa o qui-quadrado para padronizar os valores de contingência e formar a base para a associação ou similaridade.
Está correto o que se afirma APENAS em

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 1

   ×

   Para resolver à questão use, das informações dadas a seguir, as que julgar apropriadas.Se Z tem distribuição normal padrão, então:P(Z < 0,4) = 0,655; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885 P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2,0) = 0,977; P(Z < 2,4) = 0,997Seja

   

   uma variável aleatória normal bivariada com vetor de médias

   

   e matriz de covariâncias

   

   Fechar

(1,0) 5 - 

Sejam f(k) e h(k), k = 1,2,3,..., respectivamente, as funções de autocorrelação e autocorrelação parcial de um modelo ARIMA(p,d,q). Considere as seguintes afirmações: I. No modelo ARIMA(0,d,1), a região de admissibilidade do modelo é −1 < θ < 1, onde θ é o parâmetro de médias móveis do modelo. II. No modelo ARMA(0,d, 2), f(1) = f(2) e f(k) = 0 para k > 2 III. No modelo ARIMA(1,d,1) f(k) decai exponencialmente após k = 1 e h(k) é dominada por senoides amortecidas após k = 1. IV. No modelo ARIMA(1,d, 0) , f(1) = φ, onde φ é o parâmetro autorregressivo do modelo.
Está correto o que se afirma APENAS em

(1,0) 6 - 

A função de distribuição acumulada da variável aleatória Y que representa o número de acidentes de trabalho, por dia, em empresas do ramo metalúrgico de uma determinada região é dada por: 

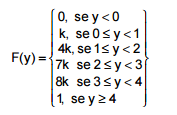
Sabendo que a média da variável aleatória Y é 2 dias, o valor da variância de Y, em (dias)², é

(1,0) 7 - 

Considere as variáveis aleatórias X_i , i = 1 ou i = 2, dadas pelas condições e definições I e II abaixo. I. Suponha que ao realizar um experimento ocorra o evento A com probabilidade p1 e não ocorra A com probabilidade (1 − p1). Repete-se o experimento até que A ocorra pela primeira vez. Seja X₁ a variável aleatória que representa o número de repetições do experimento até que A ocorra pela primeira vez. II. Suponha que ao realizar um experimento ocorra o evento B com probabilidade p2 e não ocorra B com probabilidade (1 − p₂). Repete-se o experimento até que B ocorra pela segunda vez. Seja X₂ a variável aleatória que representa o número de repetições do experimento até que B ocorra pela segunda vez.
Sabendo que P(X₁ = 2) = 0,24, que p₁ < 0,5 e que p₂ = 0,75p₁, o valor da probabilidade P(X₂ > 3) é igual a

(1,0) 8 - 

Suponha que o número de acidentes de trabalho, por mês, em montadoras de veículos de certa região tem distribuição de Poisson com média de λ acidentes por mês. Suponha que a probabilidade de ocorrerem 3 acidentes é o dobro da probabilidade de ocorrerem 4 acidentes, no mesmo período. Nessas condições, a probabilidade de ocorrer mais de um acidente no período de 24 dias é igual a
Dados: e^-1 =0,37 e^-1,6=0,20 e^-3=0,05

(1,0) 9 - 

Suponha que a variável X, que representa o tempo de vida, em horas, do vírus da gripe em superfícies não porosas como metal, plástico e madeira, tenha distribuição exponencial com média de 10 horas. Nessas condições, P(X < 8 horas) é igual a Dados: e^-0,8 =0,45 e^-0,4=0,67 e^-1=0,37

(1,0) 10 - 

Em determinada empresa existem 3 departamentos A, B e C com 10, 6 e 4 funcionários, respectivamente. Uma comissão de 3 funcionários será selecionada dentre todos os 20 funcionários com o objetivo de estabelecer regras de melhoria relativas a acidentes de trabalho na empresa. Se a seleção for aleatória, a probabilidade da comissão ser constituída por dois funcionários de A e um de C é igual a

(1,0) 11 - 

Considere as informações e os dados abaixo para responder à questão.A tabela a seguir apresenta a distribuição de frequências conjunta das variáveis salário e tempo de serviço, relativas a um grupo de 200 funcionários de um órgão público. A variável salário está representada por faixas de salário em número de salários mínimos (SM) e a variável tempo de serviço foi classificada por faixas de tempo em anos.

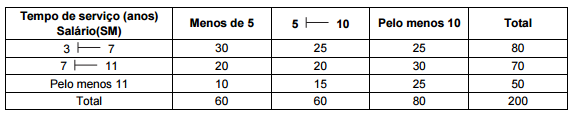
Quatro funcionários serão selecionados ao acaso e com reposição desse grupo. A probabilidade de que, exatamente, dois tenham salários na faixa de 7

11 (SM) ou tenham tempo de serviço de, pelo menos, 10 anos é igual a

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 1

   ×

   Para resolver à questão use, das informações dadas a seguir, as que julgar apropriadas.Se Z tem distribuição normal padrão, então:P(Z < 0,4) = 0,655; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885 P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2,0) = 0,977; P(Z < 2,4) = 0,997Seja

   

   uma variável aleatória normal bivariada com vetor de médias

   

   e matriz de covariâncias

   

   Fechar

(1,0) 12 - 

Cinco funcionários serão selecionados ao acaso e com reposição desse grupo. A probabilidade de que, nesse grupo de cinco, três funcionários tenham menos do que 5 anos de serviço e que dois funcionários tenham, pelo menos, 10 anos de serviço é igual a

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 1

   ×

   Para resolver à questão use, das informações dadas a seguir, as que julgar apropriadas.Se Z tem distribuição normal padrão, então:P(Z < 0,4) = 0,655; P(Z < 1) = 0,841; P(Z < 1,2) = 0,885 P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2,0) = 0,977; P(Z < 2,4) = 0,997Seja

   

   uma variável aleatória normal bivariada com vetor de médias

   

   e matriz de covariâncias

   

   Fechar

(1,0) 13 - 

Um funcionário desse grupo será selecionado ao acaso. A probabilidade dele ganhar, pelo menos, 11 salários mínimos, dado que ele trabalha há menos de 10 anos no órgão público, é igual a

(1,0) 14 - 

Um quadro de análise de variância forneceu as seguintes informações em que ficaram omitidos diversos dados importantes como, por exemplo, as respectivas somas de quadrados “entre grupos” e “dentro dos grupos”:
Fonte de variação Soma de quadrados F (F calculado) Entre grupos m 7,5 Dentro dos grupos n Total 117
Este quadro refere-se a um estudo cujo objetivo é testar a hipótese de igualdade das médias de um determinado atributo, a um nível de significância α, correspondente a 4 grupos, independentes, cada um contendo 10 observações obtidas aleatoriamente. O valor de m é igual a

1. Texto da questão (clique para ver)

   Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística 2

   ×

   Para resolver a questão considere que (10,0; 27,5) é um ponto pertencente à reta de equação y = a + bx, correspondente ao modelo de regressão linear simples yi = α + βxi + εi (i = 1, 2, 3, ...), em que:I. yi é o salário do trabalhador i em um determinado país, em unidades monetárias.II. xi é o número de anos de experiência do trabalhador i.III. α e β são parâmetros desconhecidos com suas estimativas (a e b, respectivamente) obtidas pelo método dos mínimos quadrados e com base em 20 pares de observações (xi , yi ).IV. εi é o erro aleatório com as respectivas hipóteses consideradas do modelo de regressão linear simples.

   

   Fechar

(1,0) 15 - 

Considerando os parâmetros obtidos pelo método dos mínimos quadrados e o respectivo quadro de análise de variância, são dadas as seguintes informações: I. O coeficiente de explicação (R²), definido como sendo o resultado da divisão da variação explicada pela variação total, é superior a 80%. II. A estimativa da variância do modelo teórico (σ²) é igual a 2,5. III. O valor da estatística F (F calculado) obtido para comparação com o F tabelado com os respectivos graus de liberdade no numerador e no denominador é igual a 41. IV. A cada ano adicional de experiência do trabalhador, o acréscimo do salário em unidades monetárias (A) é tal que 1 < A < 2.
Está correto o que se afirma APENAS em