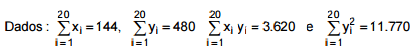Simulado TRT 20° REGIÃO (SE | Analista Judiciário – Estatística | CONCURSO
📚 Simulado TRT 20ª Região | Analista Judiciário - Estatística | cód.7909
Não deixe a preparação para depois. Treine com o simulado TRT 20ª Região hoje mesmo! ⏱️
🔗 Vejam mais simulados TRT 20ª Região
🎯 São milhares de simulados para concurso disponíveis para você praticar e conseguir a tão sonhada aprovação em Concurso Público.
🧪 Este Simulado TRT 20ª Região foi elaborado da seguinte forma:
- 📌 Categoria: Concurso
- 🏛️ Instituição: TRT 20ª Região
- 👔 Cargo: Analista Judiciário - Estatística
- 📚 Matéria: Estatística
- 🧩 Assuntos do Simulado:
- 🏢 Banca Organizadora: FCC
- ❓ Quantidade de Questões: 20
- ⏱️ Tempo do Simulado: 60 minutos
⚙️ REGRA DO SIMULADO
Este simulado é gratuito 🆓. Basta clicar no botão iniciar abaixo e preencher um breve cadastro para participar do nosso ranking.
📊 No ranking você compara sua nota com outros candidatos e acompanha sua evolução nos estudos.
🚀 Aproveite este simulado TRT 20ª Região e saia na frente na sua preparação!
📖 Questões TRT 20ª Região
Se ainda não estiver pronto para fazer o simulado, treine antes com nossas questões de concursos:
Questões do concurso TRT 20ª Região
🎥 Vídeo Aula
Confira vídeo aulas no YouTube com foco no concurso TRT 20ª Região. Estude com conteúdo gratuito e atualizado.
Assistir vídeo aula sobre TRT 20ª Região
📚 Apostila
Encontre apostilas completas e materiais didáticos atualizados para o concurso TRT 20ª Região.
Ver apostilas para TRT 20ª Região
📢 Concursos Abertos para TRT 20ª Região
Veja os concursos abertos da instituição TRT 20ª Região. A lista está sempre atualizada:
Concursos abertos para TRT 20ª Região
🍀 Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z ✅
- #117552
- Banca
- FCC
- Matéria
- Estatística
- Concurso
- TRT 20ª Região
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 16 -
Considerando a equação da reta obtida pelo método dos mínimos quadrados, tem-se que a estimativa do salário de um trabalhador com 16 anos de experiência é, em unidades monetárias, de
- a) 33,50
- b) 40,00
- c) 30,75
- d) 25,00
- e) 35,00
- #117553
- Banca
- FCC
- Matéria
- Estatística
- Concurso
- TRT 20ª Região
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 17 -
Uma amostra aleatória de tamanho 7 foi extraída, com reposição, de uma população e abaixo foram registrados os valores da amostra (em ordem crescente). {6,25; 6,55; 6,90; 7,05; 7,10; 7,20; 7,25}
Sabendo-se que o intervalo [6,55; 7,20] constitui um intervalo de confiança da mediana da respectiva população, então o nível de confiança deste intervalo é igual a
- a) 98,75%
- b) 84,00%
- c) 87,50%
- d) 95,00%
- e) 93,75%
- #117554
- Banca
- FCC
- Matéria
- Estatística
- Concurso
- TRT 20ª Região
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 18 -
Com a utilização do teste do qui-quadrado, deseja-se averiguar se a variância (σ2) de uma população normalmente distribuída e de tamanho infinito é igual a 2. Uma amostra aleatória de tamanho 19 é extraída desta população obtendo-se uma variância amostral igual a 2,25. Foram formuladas então as hipóteses H0: σ2 = 2 (hipótese nula) e H1: σ2 ≠ 2 (hipótese alternativa). Admitindo-se um nível de significância α e efetuando-se o teste de significância bilateral, tem-se, com base nos dados da amostra, que o valor da estatística x2calc (qui-quadrado calculado) utilizado para a conclusão do teste é igual a
- a) 21,375
- b) 13,500
- c) 24,000
- d) 20,250
- e) 18,750
- #117555
- Banca
- FCC
- Matéria
- Estatística
- Concurso
- TRT 20ª Região
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 19 -
Uma população de tamanho infinito tem distribuição normal com média μ e variância 16. A fim de proceder ao teste da hipótese: H0: μ = 10 (hipótese nula) contra a hipótese H1: μ ≠ 10 (hipótese alternativa), ao nível de significância α, é extraída uma amostra aleatória de tamanho 256 da população. O valor encontrado para a média amostral foi de 10,55. Considere que na curva normal padrão (Z) as probabilidades P(Z > 1,96) = 0,025 e P(Z > 2,58) = 0,005. É correto afirmar então que H0
- a) é rejeitada tanto ao nível de significância de 1%, como ao nível de significância de 5%.
- b) não é rejeitada para qualquer nível de significância inferior a 1%.
- c) não é rejeitada para qualquer nível de significância superior a 5%.
- d) não é rejeitada para 0,01 < α < 0,05.
- e) é rejeitada ao nível de significância de 1% e não é rejeitada ao nível de significância de 5%.
- #117556
- Banca
- FCC
- Matéria
- Estatística
- Concurso
- TRT 20ª Região
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 20 -
Em um processo de fabricação de um equipamento admite-se que 10% saem defeituosos quando este processo está sob controle. Para testar se o processo está sob controle são escolhidos aleatoriamente, com reposição, 4 equipamentos da produção, tomando-se como decisão que o processo está fora de controle se o número de equipamentos defeituosos for maior que 2. Chamando de p a proporção de equipamentos defeituosos e considerando as hipóteses H0: p = 0,1 (hipótese nula) e H1: p = 0,2 (hipótese alternativa), obtém-se que o nível de significância do teste e a potência do teste são, respectivamente,
- a) 0,10% e 0,80%
- b) 0,46% e 3,20%
- c) 2,72% e 0,80%
- d) 2,72% e 2,72%
- e) 0,37% e 2,72%