Analisando os dados do gráfico, o valor do ingresso individual que fornece a máxima receita para o parque temático é de
Simulado IF/RN - Matemática | CONCURSO
OBJETIVOS | Simulado IF/RN - Matemática
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores concursos públicos do país, através de simulados, provas e questões de concursos.
PÚBLICO ALVO | Simulado IF/RN - Matemática
Candidatos e/ou concursandos, que almejam aprovação em concursos públicos de nível Médio do concurso IF/RN.
SOBRE AS QUESTÕES | Simulado IF/RN - Matemática
Este simulado contém questões da banca FUNCERN , para nível Médio do cargo de Assistente Administrativo. Auxiliando em sua aprovação no concurso público escolhido. Utilizamos provas de concursos anteriores, conforme editais mais recentes IF/RN.
*Conteúdo Programático do Simulado IF/RN - Matemática.
Matemática
- Nem todos os assuntos serão abordados neste simulado de prova e questões de Matemática.
- #43598
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
- a) 16/19
- b) 17/19
- c) 27/38
- d) 29/38
- #43599
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
- a) cos x < sen 2x < cos 2x
- b) sen 2x < cos 2x < cos x
- c) cos 2x < cos x < sen x
- d) sen 2x < cos x < sen x
- #43600
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
A hipotenusa do triângulo retângulo ABC da figura abaixo mede 8 cm.

Se M é o ponto médio do segmento AC, a área do triângulo retângulo vale
- a) 4√2 cm².
- b) 4√3 cm².
- c) 8√2 cm².
- d) 8√3 cm².
- #43601
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
O gráfico a seguir mostra a variação da quantidade de visitantes mensais em um parque temático em função do valor do ingresso individual, cobrado na entrada.

Fonte: FUNCERN, 2015.
Analisando os dados do gráfico, o valor do ingresso individual que fornece a máxima receita para o parque temático é de
- a) R$ 22,50.
- b) R$ 20,50.
- c) R$ 21,25.
- d) R$ 25,25.
- #43602
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
- a) 5,00.
- b) 5,50.
- c) 6,00.
- d) 6,50.
- #43603
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
- a) 1
- b) 2
- c) 3
- d) 4
- #43604
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -

- a) P(A) + P(B) é menor que 70%
- b) P(C) + P(D) é menor que 15%
- c) P(B) + P(C) > P(A) + P(D)
- d) P(B) + P(C) + P(D) > P(A)
- #43605
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
As funções f e g, definidas por f : IR – {2}? IR e g : IR ? IR, são tais que f(x) =
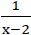
e g(x) = x² – 2x + 1.
Considerando essas informações, g[f(2+?2)] ? f [g(?3+1)] é igual a
- a)
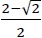
- b)

- c)

- d)

- #43606
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
- a) 6.000
- b) 11.286
- c) 45.144
- d) 2.193.360
- #43607
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Se M representa a matriz
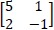
, N a matriz
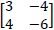
e Xt a transposta da matriz X, a soma de todos os elementos da matriz produto P = M.Nt é igual a
- a) 15.
- b) 27.
- c) 34.
- d) 49.
- #43608
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 11 -
- a) 7
- b) 9
- c) 11
- d) 15
- #43609
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 12 -

- a) 80π cm³.
- b) 90π cm³.
- c) 100π cm³.
- d) 110π cm³.
- #43610
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 13 -
- a) 30 cm.
- b) 35,5 cm.
- c) 37,5 cm.
- d) 40 cm.
- #43611
- Banca
- FUNCERN
- Matéria
- Matemática
- Concurso
- IFRN
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 14 -
- a) R$ 20,00
- b) R$ 26,00
- c) R$ 30,00
- d) R$ 32,00

