Simulado ENEM | Matemática | ENEM

(1,0) 1 - 

A inclinação de um telhado depende do tipo e da marca das telhas escolhidas. A figura é o esboço do telhado da casa de um específico proprietário. As telhas serão apoiadas sobre a superfície quadrada plana ABCD, sendo BOC um triângulo retângulo em O. Sabe-se que h é a altura do telhado em relação ao forro da casa (a figura plana ABOE), b = 10 é o comprimento do segmento OB, e d é a largura do telhado (segmento AB), todas as medidas dadas em metro.

Sabe-se que, em função do tipo de telha escolhida pelo proprietário, a porcentagem i de inclinação ideal do telhado, descrita por meio da relação é de 40%, e que a expressão que determina o número N de telhas necessárias na cobertura é dada por N = d2 x 10,5. Além disso, essas telhas são vendidas somente em milheiros.

O proprietário avalia ser fundamental respeitar a inclinação ideal informada pelo fabricante, por isso argumenta ser necessário adquirir a quantidade mínima de telhas correspondente a

(1,0) 2 - 

A figura a seguir representa parte da planta de um loteamento, em que foi usada a escala 1 : 1 000. No centro da planta uma área circular, com diâmetro de 8 cm, foi destinada para a construção de uma praça. 

O diâmetro real dessa praça, em metro, é:

(1,0) 3 - 

Um comerciante abrirá um supermercado, no mês de outubro, e precisa distribuir 5 produtos de limpeza em uma gôndola de cinco prateleiras que estão dispostas uma acima da outra (um tipo de produto por prateleira). Ele sabe que a terceira prateleira oferece uma melhor visibilidade dos produtos aos clientes.

Ele fez uma pesquisa sobre o número de vendas desses produtos, nos meses de agosto e setembro, em uma loja da concorrência (mostrada a seguir), e pretende incrementar suas vendas, em relação a seu concorrente, colocando na terceira prateleira de seu supermercado o produto que teve o maior índice de aumento nas vendas no mês de setembro em relação ao mês de agosto, na loja concorrente.

O comerciante deve colocar na terceira prateleira o produto número

(1,0) 4 - 

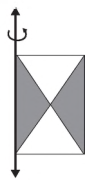
A figura mostra uma anticlepsidra, que é um sólido geométrico obtido ao se retirar dois cones opostos pelos vértices de um cilindro equilátero, cujas bases coincidam com as bases desse cilindro. A anticlepsidra pode ser considerada, também, como o sólido resultante da rotação de uma figura plana em torno de um eixo.

A figura plana cuja rotação em torno do eixo indicado gera uma anticlepsidra como a da figura acima é

(1,0) 5 - 

Em março de 2011, um terremoto de 9,0 graus de magnitude na escala Richter atingiu o Japão matando milhares de pessoas e causando grande destruição. Em janeiro daquele ano, um terremoto de 7,0 graus na escala Richter atingiu a cidade de Santiago Del Estero, na Argentina. A magnitude de um terremoto, medida A pela escala Richter, é em que A é a amplitude do movimento vertical do° solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.

Disponível em: http://earthquake.usgs.gov. Acesso em: 28 fev. 2012 (adaptado).

A razão entre as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina é

(1,0) 6 - 

Em um jogo de tabuleiro, a pontuação é marcada com fichas coloridas. Cada ficha vermelha vale um ponto. Três fichas vermelhas podem ser trocadas por uma azul, três fichas azuis podem ser trocadas por uma branca, e três fichas brancas podem ser trocadas por uma verde. Ao final do jogo, os jogadores A, B e C terminaram, cada um, com as quantidades de fichas, conforme a tabela seguinte:

De acordo com essa tabela, as classificações em primeiro, segundo e terceiro lugares ficaram, respectivamente, para os jogadores

(1,0) 7 - 

Um automóvel pode ser abastecido com os combustíveis A ou B e tem capacidade para armazenar T litro. O quadro indica os preços e mostra o rendimento desse automóvel, por litro, quando abastecido com esses combustíveis.

O dono desse automóvel estabelece duas estratégias de viagem. Em ambas ele irá abastecer duas vezes. O primeiro abastecimento é feito a partir do tanque vazio e o reabastecimento é feito quando o tanque esvaziar novamente.

1ª estratégia de viagem: abastecer meio tanque com o combustível A e depois abastecer um quarto de tanque com o combustível B.

2ª estratégia de viagem: abastecer meio tanque com o combustível B e depois abastecer um quarto de tanque com o combustível A.

O custo (C) da estratégia que possibilita percorrer a maior distância é

(1,0) 8 - 

Em certa página de um livro foi anotada uma senha. Para se descobrir qual é a página, dispõe-se da informação de que a soma dos quadrados dos três números correspondentes à página da senha, à página anterior e à página posterior é igual a um certo número k que será informado posteriormente.

Denotando por n o número da página da senha, qual é a expressão que relaciona n e k?

(1,0) 9 - 

Um brinquedo chamado pula-pula, quando visto de cima, consiste de uma cama elástica com contorno em formato de um hexágono regular.

Se a área do círculo inscrito no hexágono é 3? metros quadrados, então a área do hexágono, em metro quadrado, é

(1,0) 10 - 

Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.

Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy.

A equação da parábola que representa a trajetória descrita pelo projétil é

(1,0) 11 - 

Um quebra-cabeça consiste em recobrir um quadrado com triângulos retângulos isosceles, como ilustra a figura.

Uma artesã confecciona um quebra-cabeça como o descrito, de tal modo que a menor das peças é um triângulo retângulo isosceles cujos catetos medem 2 cm.

O quebra-cabeça, quando montado, resultará em um quadrado cuja medida do lado, em centímetro, é

(1,0) 12 - 

Devido ao não cumprimento das metas definidas para a campanha de vacinação contra a gripe comum e o vírus H1N1 em um ano, o Ministério da Saúde anunciou a prorrogação da campanha por mais uma semana. A tabela apresenta as quantidades de pessoas vacinadas dentre os cinco grupos de risco até a data de início da prorrogação da campanha.

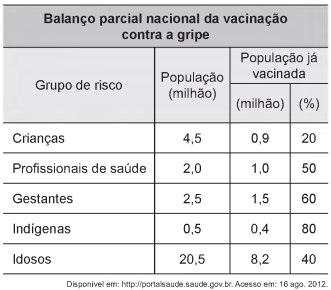
Qual é a porcentagem do total de pessoas desses grupos de risco já vacinadas?

(1,0) 13 - 

O atleta 10 irá realizar o último salto da final. Ele observa no Quadro 1, antes de executar o salto, o recorte do quadro parcial de notas com a sua classificação e a dos três primeiros lugares até aquele momento.

O atleta optará pelo salto com a maior probabilidade de obter a nota estimada, de maneira que lhe permita alcançar o primeiro lugar.

Considerando essas condições, o salto que o atleta deverá escolher é o de tipo

(1,0) 14 - 

Uma loja vende automóveis em N parcelas iguais sem juros. No momento de contratar o financiamento, caso o cliente queira aumentar o prazo, acrescentando mais 5 parcelas, o valor de cada uma das parcelas diminui R$ 200,00, ou se ele quiser diminuir o prazo, com 4 parcelas a menos, o valor de cada uma das parcelas sobe R$ 232,00. Considere ainda que, nas três possibilidades de pagamento, o valor do automóvel é o mesmo, todas são sem juros e não é dado desconto em nenhuma das situações.

Nessas condições, qual é a quantidade N de parcelas a serem pagas de acordo com a proposta inicial da loja?

(1,0) 15 - 

Com o avanço em ciência da computação, estamos próximos do momento em que o número de transistores no processador de um computador pessoal será da mesma ordem de grandeza que o número de neurônios em um cérebro humano, que é da ordem de 100 bilhões.

Uma das grandezas determinantes para o desempenho de um processador é a densidade de transistores, que é o número de transistores por centímetro quadrado. Em 1986, uma empresa fabricava um processador contendo 100 000 transistores distribuídos em 0,25 cm2 de área. Desde então, o número de transistores por centímetro quadrado que se pode colocar em um processador dobra a cada dois anos (Lei de Moore).

Disponível em: www.pocket-lint.com. Acesso em: 1 dez. 2017 (adaptado).

Considere 0,30 como aproximação para log102.

Em que ano a empresa atingiu ou atingirá a densidade de 100 bilhões de transistores?