Geometria Espacial: Explorando o Mundo Tridimensional

A Geometria Espacial, um ramo da matemática que se dedica ao estudo de figuras com mais de duas dimensões, constitui um campo de conhecimento essencial para compreender as propriedades e relações no espaço tridimensional. Suas origens remontam à Grécia Antiga e à Mesopotâmia, por volta de 1000 a.C., onde conceitos primitivos começaram a ser delineados. Inicialmente vinculada à Metafísica e à religião, a Geometria Espacial ganhou proeminência com a obra "Elementos" de Euclides, que consolidou os conhecimentos geométricos da época.

O ressurgimento do estudo da Geometria Espacial na Idade Média marcou um período de avanços significativos, impulsionado pelas contribuições de matemáticos notáveis. Leonardo Fibonacci, por exemplo, desempenhou um papel crucial ao escrever a "Practica Geometriae". Posteriormente, Joannes Kepler, no século XVII, classificou o "Steometria" como o cálculo de volume, adicionando novas perspectivas à disciplina e ampliando seu escopo.

Essa trajetória histórica evidencia a importância da Geometria Espacial como uma ferramenta fundamental para desvendar as complexidades do espaço tridimensional, com aplicações que transcendem a matemática pura, influenciando campos como arquitetura, engenharia e ciências naturais.

Índice

1. Características da Geometria Espacial
2. Figuras Geométricas Espaciais
   • Cubo
   • Dodecaedro
   • Tetraedro
   • Octaedro
   • Icosaedro
   • Prisma
   • Pirâmide
3. Curiosidades

Características da Geometria Espacial

A Geometria Espacial, como disciplina matemática, concentra-se no estudo aprofundado de objetos tridimensionais, conhecidos como "sólidos geométricos" ou "figuras geométricas espaciais". Essa área de conhecimento vai além da simples análise da forma externa desses objetos, estendendo-se à compreensão de suas características intrínsecas e à aplicação de cálculos que envolvem volumes, representando, assim, o espaço que essas figuras ocupam.

O ponto de partida na Geometria Espacial envolve a compreensão dos conceitos fundamentais, como ponto, reta, linha e plano. Esses elementos são a base para a construção de estruturas mais complexas no espaço tridimensional. O ponto, por exemplo, é o conceito mais elementar, sendo adimensional e representando apenas a localização no espaço. A reta, composta por infinitos pontos, é uma estrutura infinita nos dois lados, determinando a distância mais curta entre dois pontos específicos.

Já a linha, embora compartilhe algumas características com a reta, possui a propriedade adicional de formar curvas e nós sobre si mesma. Por fim, o plano, outra estrutura infinita, estende-se em todas as direções, formando a base para diversas figuras geométricas espaciais.

Nesse contexto, os conceitos básicos são essenciais não apenas para a descrição das figuras tridimensionais, mas também para estabelecer relações e propriedades que permitam uma análise mais profunda dessas formas. A Geometria Espacial desempenha um papel crucial na construção do conhecimento matemático, fornecendo ferramentas para visualizar e compreender o espaço tridimensional de maneira mais abrangente. Essa compreensão, por sua vez, contribui para a resolução de problemas práticos e abstratos, consolidando a importância dessa disciplina no contexto matemático e científico.

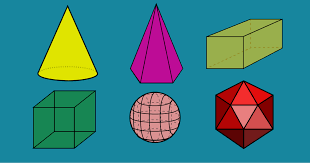
Figuras Geométricas Espaciais

A Geometria Espacial abrange diversas figuras tridimensionais, cada uma com propriedades e características únicas. Vamos explorar algumas delas em detalhes:

Cubo: O cubo é um hexaedro regular composto por 6 faces quadrangulares, 12 arestas e 8 vértices. Suas características específicas incluem uma área lateral de 4×24�24×24a2, área total de 6×24�26×24a2 e volume de 3�33​a3.

Dodecaedro: O dodecaedro é um poliedro regular que possui 12 faces pentagonais, 30 arestas e 20 vértices. Sua área total é 325+105�2325+105​​a2 e o volume é 14(15+75)�341​(15+75​)a3.

Tetraedro: O tetraedro, por sua vez, é um poliedro regular composto por 4 faces triangulares, 6 arestas e 4 vértices. Sua área total é 4�23444a23​​, e o volume é 13��⋅ℎ31​Ab⋅h.

Octaedro: O octaedro, também poliedro regular, possui 8 faces formadas por triângulos equiláteros, 12 arestas e 6 vértices. Sua área total é 2×3�22×3​a2, e o volume é 13�3231​a32​.

Icosaedro: Composto por 20 faces triangulares, 30 arestas e 12 vértices, o icosaedro é um poliedro convexo. Sua área total é 53�253​a2, e o volume é 512(3+5)�3125​(3+5​)a3.

Prisma: O prisma é um poliedro com duas faces paralelas formando a base. Pode ter bases triangulares, quadrangulares, pentagonais, hexagonais, entre outras. Sua área da base é ��Ab, a área lateral é 6�⋅ℎ6a⋅h, a área total é 32��23​Ab e o volume é ��⋅ℎAb⋅h.

Pirâmide: Por fim, a pirâmide é um poliedro com uma base (que pode ser triangular, pentagonal, quadrada, retangular ou um paralelogramo) e um vértice que une todas as faces laterais triangulares. Sua área total é ��+��Al+Ab, e o volume é 13��⋅ℎ31​Ab⋅h.

Cada uma dessas figuras desempenha um papel fundamental na Geometria Espacial, proporcionando uma compreensão mais profunda do espaço tridimensional e suas propriedades matemáticas. O entendimento dessas formas é crucial não apenas para o campo matemático, mas também para diversas aplicações práticas e teóricas, sendo um conhecimento relevante para possíveis avaliações, como o ENEM.

Curiosidades

A Geometria Espacial, além de suas propriedades matemáticas, traz consigo uma série de curiosidades e fatos interessantes que enriquecem ainda mais o entendimento dessa disciplina:

1. Origens da Palavra: A palavra "geometria" tem suas raízes na língua grega, resultando da união dos termos "geo" (terra) e "metria" (medida). Portanto, a Geometria pode ser literalmente entendida como a "medida da terra". Essa nomenclatura reflete a aplicação inicial da geometria no contexto prático da mensuração de terras e áreas.
2. Cálculos em Geometria Espacial: Os cálculos comuns em Geometria Espacial são abrangentes e versáteis. Além das análises de comprimentos de curvas, a disciplina lida com a determinação de áreas de superfícies e volumes de regiões sólidas. Esses cálculos têm aplicações diretas em áreas como arquitetura, engenharia e design, sendo fundamentais para compreender e modelar objetos no espaço tridimensional.
3. Outras Figuras Geométricas Espaciais: Além das figuras anteriormente mencionadas, como cubo, pirâmide e prisma, há outras formas geométricas espaciais notáveis. Cilindro, cone e esfera são exemplos dessas figuras, cada uma com suas características únicas. O cilindro, por exemplo, possui duas bases circulares e uma superfície lateral curva, enquanto o cone tem uma base circular e uma superfície lateral cônica. A esfera, por sua vez, é uma forma completamente simétrica, com todos os pontos equidistantes de seu centro.
4. Sólidos Platônicos: Os "Sólidos Platônicos" são formas geométricas especiais que têm sido conhecidas desde a antiguidade clássica. Esses sólidos são o tetraedro, o cubo, o octaedro, o dodecaedro e o icosaedro. Cada um desses sólidos tem características distintas e simetrias únicas, sendo estudados e apreciados por sua elegância matemática e significado histórico.

Essas curiosidades não apenas destacam a riqueza histórica e cultural da Geometria Espacial, mas também evidenciam a relevância prática e teórica dessa disciplina em diversos campos do conhecimento. O entendimento desses aspectos adicionais pode ser valioso em contextos educacionais, como em avaliações, incluindo o ENEM.

Como explicar geometria espacial?

A Geometria Espacial é um ramo da matemática que se dedica ao estudo das formas e propriedades dos objetos no espaço tridimensional. Para compreender esse campo, podemos dividi-lo em alguns conceitos fundamentais:

1. Dimensões Espaciais: Ao contrário da Geometria Plana, que trabalha com figuras bidimensionais, a Geometria Espacial lida com objetos que possuem três dimensões: comprimento, largura e altura. Isso inclui sólidos geométricos como cubos, pirâmides, cilindros e esferas.
2. Conceitos Primitivos: A Geometria Espacial baseia-se em conceitos primitivos como ponto, reta, linha e plano, que são fundamentais para a construção de figuras tridimensionais. Ponto representa uma posição no espaço, a reta é formada por pontos infinitos, a linha é semelhante à reta, mas pode formar curvas, e o plano é uma superfície infinita.
3. Sólidos Geométricos: Os sólidos geométricos são figuras tridimensionais que ocupam espaço. Exemplos incluem o cubo, que tem seis faces quadradas, a pirâmide, com uma base poligonal e faces triangulares, e a esfera, uma superfície curva e simétrica. O estudo desses sólidos envolve cálculos de volumes e áreas.
4. Volume e Área: Uma parte essencial da Geometria Espacial é o cálculo de volumes e áreas. O volume refere-se ao espaço ocupado por um sólido, enquanto a área está relacionada à medida da superfície do sólido. Fórmulas específicas são aplicadas a diferentes sólidos geométricos para calcular essas grandezas.
5. Aplicações Práticas: A Geometria Espacial tem aplicações práticas em diversas áreas, como arquitetura, engenharia, design e física. Arquitetos utilizam conceitos geométricos para projetar estruturas tridimensionais, enquanto engenheiros aplicam esses princípios para analisar volumes e áreas em seus projetos.
6. Sólidos Platônicos: Os sólidos platônicos são formas geométricas especiais que têm propriedades únicas e simetria. O tetraedro, cubo, octaedro, dodecaedro e icosaedro são exemplos desses sólidos, destacando-se por suas características matemáticas distintas.

Em resumo, a Geometria Espacial é uma disciplina matemática que explora as propriedades e relações de figuras tridimensionais, proporcionando uma compreensão abrangente do espaço ao nosso redor. O entendimento desses conceitos é crucial não apenas para a matemática, mas também para diversas áreas do conhecimento e aplicações práticas.

Qual é a fórmula da geometria espacial?

A Geometria Espacial envolve várias fórmulas, cada uma aplicável a diferentes sólidos geométricos para calcular áreas, volumes e outras grandezas. Abaixo estão algumas das fórmulas mais comuns:

1. Cubo:
   • Volume (V): �=�3V=a3 (onde �a é o comprimento da aresta).
   • Área da Superfície (A): �=6�2A=6a2.
2. Prisma:
   • Volume (V): �=��×ℎV=Ab×h (onde ��Ab é a área da base e ℎh é a altura).
   • Área Lateral (Al): ��=�×ℎAl=P×h (onde �P é o perímetro da base).
   • Área da Superfície (A): �=2×��+��A=2×Ab+Al.
3. Pirâmide:
   • Volume (V): �=13×��×ℎV=31​×Ab×h (onde ��Ab é a área da base e ℎh é a altura).
   • Área Total (At): ��=��+��At=Ab+Al (onde ��Al é a área lateral).
4. Cilindro:
   • Volume (V): �=��2×ℎV=πr2×h (onde �r é o raio da base e ℎh é a altura).
   • Área Lateral (Al): ��=2×�×�×ℎAl=2×π×r×h.
   • Área da Superfície (A): �=2×�×�×(�+ℎ)A=2×π×r×(r+h).
5. Esfera:
   • Volume (V): �=43×�×�3V=34​×π×r3 (onde �r é o raio).
   • Área da Superfície (A): �=4×�×�2A=4×π×r2.

Essas fórmulas são apenas algumas das muitas utilizadas na Geometria Espacial. Cada sólido geométrico tem suas próprias características e, portanto, fórmulas específicas para calcular diferentes propriedades.

Quais são as principais figuras da geometria espacial?

As principais figuras da Geometria Espacial são os sólidos geométricos tridimensionais, também chamados de figuras geométricas espaciais. Alguns dos mais importantes incluem:

1. Cubo:
   • Um hexaedro regular com 6 faces quadrangulares, 12 arestas e 8 vértices.
2. Dodecaedro:
   • Um poliedro regular com 12 faces pentagonais, 30 arestas e 20 vértices.
3. Tetraedro:
   • Um poliedro regular com 4 faces triangulares, 6 arestas e 4 vértices.
4. Octaedro:
   • Um poliedro regular com 8 faces formadas por triângulos equiláteros, 12 arestas e 6 vértices.
5. Icosaedro:
   • Um poliedro convexo com 20 faces triangulares, 30 arestas e 12 vértices.
6. Prisma:
   • Um poliedro com duas faces paralelas que formam a base. Pode ter bases triangulares, quadrangulares, pentagonais, hexagonais, entre outras.
7. Pirâmide:
   • Um poliedro com uma base (triangular, pentagonal, quadrada, retangular, paralelogramo) e um vértice que une todas as faces laterais triangulares.
8. Cilindro:
   • Um sólido com duas bases circulares paralelas e uma superfície lateral curva.
9. Cone:
   • Semelhante ao cilindro, mas com uma base circular e uma superfície lateral que converge para um vértice.
10. Esfera:
    • Uma superfície tridimensional completamente redonda, onde todos os pontos na superfície estão a uma distância constante do centro.

Essas figuras são essenciais para o estudo da Geometria Espacial e têm propriedades distintas que podem ser analisadas e calculadas usando fórmulas específicas.

Quais são os tipos de geometria espacial?

Os principais tipos de Geometria Espacial são:

1. Geometria Espacial Euclidiana:
   • É a forma tradicional de geometria espacial que segue os postulados e axiomas propostos por Euclides, um matemático grego. Ela lida com o espaço tridimensional, explorando as propriedades e relações entre pontos, retas, planos e sólidos geométricos.
2. Geometria Analítica Espacial:
   • Utiliza conceitos da álgebra linear e da análise para estudar as figuras geométricas no espaço. As coordenadas tridimensionais são frequentemente empregadas para representar pontos e realizar cálculos.
3. Geometria Projetiva Espacial:
   • Expande as ideias da geometria projetiva para o espaço tridimensional. Ela examina as propriedades geométricas que permanecem inalteradas sob transformações projetivas, abstraindo conceitos como ponto, reta e plano.
4. Geometria Descritiva:
   • Desenvolvida para representar objetos tridimensionais em um plano bidimensional, útil para engenheiros, arquitetos e designers. Ela usa projeções e técnicas específicas para mostrar as características de objetos espaciais em desenhos técnicos.

Cada uma dessas abordagens oferece perspectivas únicas e ferramentas específicas para explorar e compreender a Geometria Espacial, adaptando-se a diferentes necessidades e aplicações.