Função afim
Função afim
Entenda e aprenda oque é função afim!
A função afim, também chamada de função do 1º grau, é uma função f : ℝ→ℝ, definida como f(x) = ax + b, sendo a e b números reais. As funções f(x) = x + 5, g(x) = 3√3x - 8 e h(x) = 1/2 x são exemplos de funções afim.
Neste tipo de função, o número a é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. Já o número b é chamado de termo constante.
A função afim, ou função do 1º grau, é uma função f : ℝ→ℝ, definida como f(x) = ax + b, sendo a e b números reais. As funções f(x) = x + 5, g(x) = 3√3x - 8 e h(x) = 1/2 x são exemplos de funções afim.
Neste tipo de função, o número a é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. Já o número b é chamado de termo constante.
VEJA TAMBÉM
- Coeficientes da Função Afim
- FUNÇÃO IDENTIDADE
- Função constante
- Função linear
- Translação da função identidade
- Provas Enem
- Questões Enem
- Simulado Enem

Coeficientes da Função Afim
Em f(x)= ax +b, o valor de a é identificado como taxa de variação (crescimento) ou de coeficiente angular porque aponta o quanto a função pode crescer e a inclinação da reta em relação ao eixo da abscissa (x) no plano cartesiano.
Já o termo b, que é constante, é identificado como coeficiente linear da função porque define o ponto onde a reta corta o eixo y do gráfico quando x = 0. Em f(x) = 3x + 10 a função irá cortar o eixo das ordenadas (y) no ponto (0,10), pois f(0) = 3.0+10 = 10.
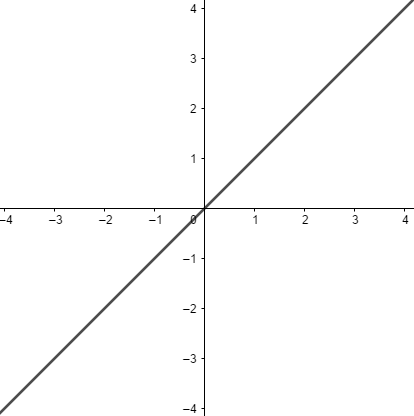
FUNÇÃO IDENTIDADE
Seja uma função f:R→R definida por f(x) = x. Então, neste caso se a = 1 e b = 0, o gráfico de uma função identidade é chamada de bissetriz dos quadrantes impares, que passam pelo 1º e 3º quadrante e na origem do eixo cartesiano (0, 0).
Função constante
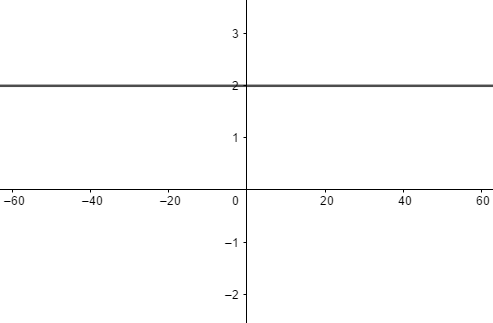
Uma função f:R→R é dita constante quando f(x) = b, logo a = 0. Seu gráfico será sempre uma reta paralela ao eixo x e que intercepta o eixo y num ponto b.
Por exemplo, seja a função f(x) = 2, o seu gráfico será:
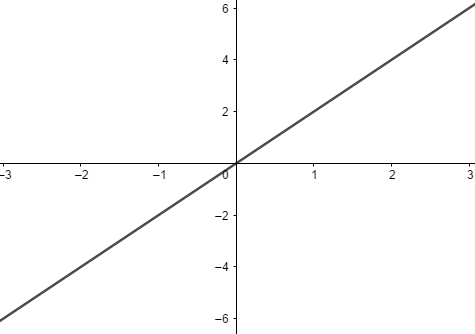
Função linear
Uma função f:R→R é dita constante quando f(x) = ax, logo b = 0. Seu gráfico será sempre uma reta paralela que intercepta a origem do eixo cartesiano. Por exemplo, a função f(x) = 2x terá a sua representação gráfica dada por:
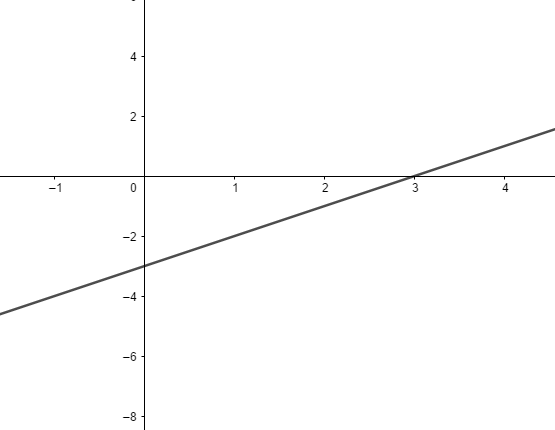
Translação da função identidade
Se tomarmos a função identidade e acrescentarmos à ela um coeficiente linear e mantendo o seu coeficiente angular igual a 1, ocorrerá a translação da reta. A função será definida por f(x) = x+b sendo a = 1 e b≠0. Por exemplo, f(x)= x-3: