Simulado UFCG de Matemática | VESTIBULAR
📚 Simulado UFCG | Vestibular | cód.8072
Cada questão respondida é um passo rumo à aprovação. Bora pro simulado UFCG? 🏆
🎯 São milhares de simulados para concurso disponíveis para você praticar e conseguir a tão sonhada aprovação em Concurso Público.
🧪 Este Simulado UFCG foi elaborado da seguinte forma:
- 📌 Categoria: Vestibular
- 🏛️ Instituição: UFCG
- 👔 Cargo: Vestibular
- 📚 Matéria: Matemática
- 🧩 Assuntos do Simulado:
- 🏢 Banca Organizadora: UFCG
- ❓ Quantidade de Questões: 10
- ⏱️ Tempo do Simulado: 30 minutos
⚙️ REGRA DO SIMULADO
Este simulado é gratuito 🆓. Basta clicar no botão iniciar abaixo e preencher um breve cadastro para participar do nosso ranking.
📊 No ranking você compara sua nota com outros candidatos e acompanha sua evolução nos estudos.
🚀 Aproveite este simulado UFCG e saia na frente na sua preparação!
📖 Questões UFCG
Se ainda não estiver pronto para fazer o simulado, treine antes com nossas questões de concursos:
🎥 Vídeo Aula
Confira vídeo aulas no YouTube com foco no concurso UFCG. Estude com conteúdo gratuito e atualizado.
Assistir vídeo aula sobre UFCG
📚 Apostila
Encontre apostilas completas e materiais didáticos atualizados para o concurso UFCG.
📢 Concursos Abertos para UFCG
Veja os concursos abertos da instituição UFCG. A lista está sempre atualizada:
🍀 Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z ✅
- #120523
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
Certa espécie de animal, com população inicial de 200 indivíduos, vivendo em um ambiente limitado, capaz de suportar no máximo 500 indivíduos, é modelada pela função:
P ( t) = 100.000
200 + 300 e -2t ,onde a variável t é dada em anos. O tempo necessário para a população atingir 60 % da população máxima é:
Obs: use a aproximação onde In ( 4/9) - 0,8, onde In x representa o logaritmo natural (ou neperiano) do número real x .
- a) 0,4 anos.
- b) 0,2 anos.
- c) 0,5 anos.
- d) 0,1 anos
- e) 0,6 anos
- #120524
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
O custo de produção de um produto fabricado por uma cooperativa agrícola, em milhares de reais, é dado pela função C(x)= 4 + 6x, onde x é dado em milhares de unidades. Verificou-se que o faturamento de venda desses produtos, também em milhares de reais, é dado pela função F(x)= x2 + 3x. É correto afirmar que a cooperativa começará a ter lucro com a venda desse produto, a partir da produção de
- a) 3 milhares.
- b) 2,6 milhares.
- c) 7 milhares.
- d) 2 milhares.
- e) 4 milhares.
- #120525
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
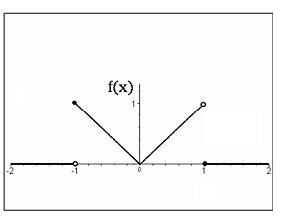
Considere uma função f (x), cujo gráfico está desenhado acima:
O gráfico que representa a função g(x) + f ( x + 1) + f ( x - 1) é
- a)
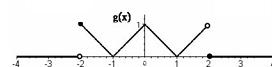
- b)
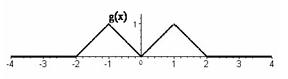
- c)
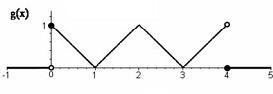
- d)
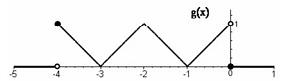
- e)
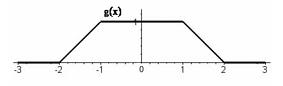
- #120526
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
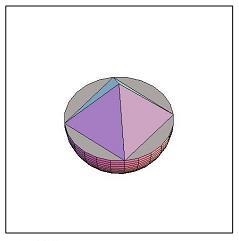
Em homenagem ao Ano Internacional da Matemática, um artista propôs a construção de uma pirâmide posicionada sobre um hemisfério. A base da pirâmide é um quadrado inscrito no círculo da base do hemisfério, como pode ser visto na figura acima. Se o volume da parte esférica e o volume da parte em forma de pirâmide são iguais, qual a razão entre o comprimento da aresta da base da pirâmide e a altura da pirâmide?
- a) π2
- b) √π3
- c) √2π
- d) √π3
- e) 32
- #120527
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Por segurança, atualmente, os números primos são importantes para criar mensagens por meio de códigos* e enviá-las via Internet. Para isso, usam-se números primos que tenham muitos dígitos. Em relação a números primos, quantos números naturais n existem de modo que n + 10/n é primo?
- a) 0
- b) 1
- c) 2
- d) 3
- e) 4
- #120528
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
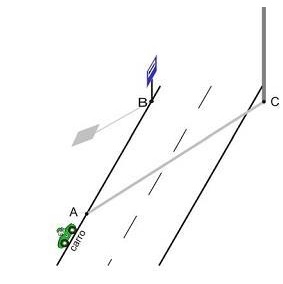
Conforme a figura acima, um carro está estacionado em uma rua plana, 2m abaixo do ponto A, que é a extremidade da sombra do poste posicionado no ponto C. Nesse instante, uma caneta de tamanho 14cm, posicionada verticalmente no solo, tem uma sombra sobre o solo de comprimento 21cm. Sabe-se que o segmento BC é perpendicular ao segmento AB, que o poste tem altura de 10m e que BC = 9 m A distância do carro ao ponto B é(está).
- a) inferior a 8m.
- b) igual a 22m.
- c) entre 8m e 10m.
- d) entre 10m e 12m.
- e) superior a 12m.
- #120529
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -

Um jornalista anuncia que, em determinado momento, o público presente em um comício realizado numa praça com formato do trapézio isósceles ABCD , com bases medindo 100m e 140m (vide figura abaixo), era de 20.000 pessoas. Sabendo-se que θ = π/4 e, considerando-se que em aglomerações desse tipo o número máximo de pessoas por metro quadrado é igual a 6, o que pode ser concluído a respeito do anúncio jornalístico?
- a) Falso, pois a praça comporta no máximo 18.000 pessoas.
- b) Falso, pois a praça comporta menos de 15.000 pessoas.
- c) Verídico, pois a praça comporta no máximo 21.000 pessoas.
- d) Falso, pois a praça comporta no máximo 19.000 pessoas.
- e) Verídico, pois a praça comporta mais de 22.000 pessoas.
- #120530
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Dois alunos estavam trabalhando com a sequência 2-5, 2-4,2-3,...218,219 , quando um outro aluno aproveitou a oportunidade e construiu uma matriz Anxn com esses números, sem repetir qualquer deles. Depois disso, lançou um desafio aos amigos, perguntando a relação entre det (2A) e det (A) Qual a resposta a esse desafio?
- a) det ( 2A) = det (A)
- b) det (2A) = 3 det (A)
- c) det (2A) = 16 det(A)
- d) det (2A) = 32 det(A)
- e) det (2A) = 81 det(A)
- #120531
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
O velocímetro do automóvel de José foi calibrado para marcar sempre uma velocidade superior à velocidade real do carro, de acordo com a seguinte tabela:

Num certo local, existe uma lombada eletrônica que fiscaliza a velocidade real máxima de 100 km/h. Qual a velocidade máxima apresentada no velocímetro do carro de José ao passar pela lombada, de modo que ele não seja multado?
- a) 103 km/h .
- b) 114,7 km/h.
- c) 113,5 km/h .
- d) 112,4 km/h.
- e) 107,3 km/h
- #120532
- Banca
- UFCG
- Matéria
- Matemática
- Concurso
- UFCG
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar