Simulado UFAC de Matematica | VESTIBULAR

(1,0) 1 - 

Considere x um número real. Dados os números complexos

e

o único caso em que ocorre a igualdade

é quando:

(1,0) 2 - 

Uma indiscutível verdade é que a Álgebra está relacionada com a maioria dos assuntos em Matemática. O rigor, a organização das idéias e o raciocínio lógico são quem melhor a definem. Um “tira-gosto” de uma aplicação à geometria, particularmente ao cálculo de área de figuras planas, está ligado à teoria dos Determinantes e inclui a regra de Sarrus para o cálculo do determinante de uma matriz quadra de ordem 3.
Mesmo não considerando estes comentários, analisando as afirmações abaixo com respeito aos pontos P = (301, 7), S = (5, -7) e Q = (400, 28) do plano, a que está correta é:

(1,0) 3 - 

Um candidato totalmente despreparado nos assuntos da Biologia compareceu para fazer as provas do Vestibular 2008/UFAC. Numa tentativa de desespero ele optou por marcar a 1ª dentre as cinco alternativas para dar a resposta para cada um dos 10 problemas de Biologia.
Se nenhuma das questões da citada prova foi anulada e com essa estratégia o candidato conseguiu acertar a resposta de apenas 4 delas, é correto afirmar que:

(1,0) 4 - 

Numa sala de aula de uma determinada escola, um professor insistia em ensinar Matemática deixando de fundamentar os conceitos que ali tratava.
Dentre algumas “verdades” usadas por ele, listadas nos itens abaixo, qual é a que não afronta as propriedades ou definições matamáticas?

(1,0) 5 - 

Considere todas as matrizes quadradas de ordem 2 cujos elementos (ou entradas) são 0 ou 1.
O número dessas matrizes que são inversíveis é:

(1,0) 6 - 

Depois de ajudar a selecionar alguns itens Emanuel dirigiu-se a um dos caixas de um supermercado. Antes de responder ao cumprimento da atendente, entregou a ela um saco de jujuba quase vazio e um quebra - cabeça que catou na seção dos brinquedos dizendo: Estas são minhas compras.
Computados os valores de todos os produtos que a família escolheu, seu pai pagou o valor de R$ 171,25 e, durante a volta para casa, mostrou-se indignado com o preço daquele jogo infantil ao comentar com a mãe do garoto que o referido brinquedo custou mais de 20% do que ele acabara de pagar.

Avalie esta situação e, sabendo que cada item pago na citada compra custou mais de R$ 2,75, determine qual dos valores abaixo poderia significar as “compras de Emanuel”.

(1,0) 7 - 

Seja x ∈ ℜ - { π⁄2 + kn; com k ∈ Z }. Então, a expressão secx.cosx - tgx.senx.cosx - cos²x , é igual a:

(1,0) 8 - 

Considere a equação (na variável x), 1 +

(x² - 6x + 9 ) =

(x - 2 ) onde ∪ = { x ∪ ℜ/ x > 2 e x ≠ 3 } é o seu conjunto universo.

As soluções desta equação são números reais tais que: ,

(1,0) 9 - 

contém finitos elementos.

(1,0) 10 - 

Considere as afirmações abaixo:

I. Sejam A e B matrizes quadradas de ordens m e n, respectivamente. A desigualdade m < n implica que o determinante da matriz A é menor que o determinante da matriz B.

II. A soma das medidas das diagonais de um polígono regular é sempre menor que o perímetro desse polígono.

III. Se a e b são números inteiros positivos quaisquer, sempre temos a desigualdade M.M.C. (a, b) > M.D.C. (a, b).

IV. Toda função ímpar é sobrejetiva.

V. O número √2 + 1/3 é irracional.

É correto afirmar que:

(1,0) 11 - 

Na figura a seguir, considere todos os quadrados de lados iguais a 2 cm. As linhas poligonais, destacadas em negrito, que ligam as figuras geométricas aos respectivos pontos, indicados pelas primeiras letras de seus nomes, tocam ou cortam os lados dos quadrados ou retângulos, sempre em seus pontos médios.

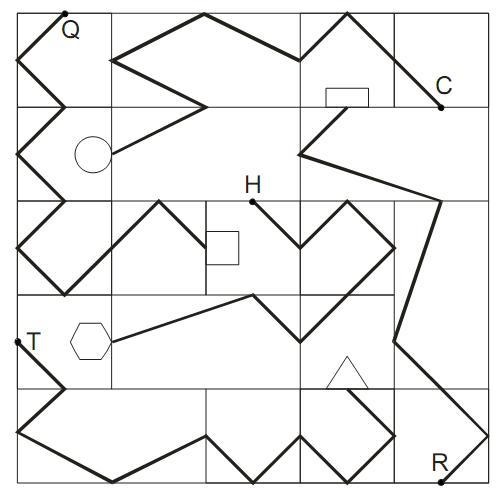
Uma estimativa correta aponta que, dentre essas, a maior linha poligonal é a que liga:

(1,0) 12 - 

Dois números x e y que satisfazem a equação y² - 10 = ³√x + y são :

(1,0) 13 - 

Cinco amigos foram a uma pizzaria. Depois de um bom bate-papo, resolveram participar do rodízio que acontecia sempre naquele dia da semana. Além de pizza, consumiram somente refrigerantes.

A conta, paga com R$ 150,00, foi dividida igualmente, cabendo para cada um deles parte dos 10% do garçom mais R$ 15,00, o preço do rodízio pago por pessoa.

Se cada um dos amigos recebeu R$ 4,50 de troco, concluímos que, em média, o valor que cada um gastou com bebida é mais próximo de:

(1,0) 14 - 

Um dado e uma urna contendo 10 bolas enumeradas de 1 a 10 são postos sobre uma mesa ampla. O dado é lançado sobre a mesa e o número m, da face que fica voltada para cima, é anotado. Em seguida, uma bola é retirada aleatoriamente da urna e o seu número n é também anotado.

A probabilidade de m + n ser um número primo é igual a:

(1,0) 15 - 

Um sujeito muito engraçado, que atende pelo apelido de “Tracajá”, tentando obter êxito nas apostas nos jogos da mega-sena, que regularmente faz aos sábados, resolveu usar a seguinte tática: escolheu 10 dezenas de modo que duas delas nunca coincidissem numa mesma coluna e, no máximo, 2 coincidissem numa mesma linha da “tabela” que contém os números de 01 a 60.

Depois de alguns minutos olhando esses números, escolheu 6 deles e fez uma única aposta, pagando por ela R$ 2,00.

Qual dos números abaixo pode representar a soma das dezenas dessa aposta feita por Tracajá, vulgo “Bicho de Casco”?