Simulado IF-RN de Matematica para Cargos diversos | CONCURSO

(1,0) 1 - 

O sistema linear

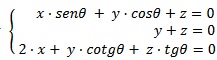
, com incógnitas x, y e z, possui infinitas soluções.

Considerando os valores de θ ∈ [0,π] tal que θ ≠ π⁄2, sendo k ∈ Z, pode-se garantir que

(1,0) 2 - 

As elipses β e ϒ cujas respectivas equações são 25x² + 16y² + 288y + 896 = 0 e x²⁄16 + y²⁄25 = 1, possuem dois pontos de intersecção.

O centro da elipse β e os pontos de intersecção serão, respectivamente,

(1,0) 3 - 

Tomando os afixos das raízes complexas de x⁶ + 1 = 0, pode-se formar um polígono no plano Argand-Gauss.
Assim, o quadrado da área desse polígono será

(1,0) 4 - 

Considere a função real f, conforme o gráfico abaixo.

O número de soluções que satisfaz a equação f(x + 2) = f(x) − 1 será

(1,0) 5 - 

Considere a matriz

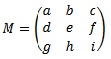
quadrada de ordem 3 cujo determinante é det M = k.

O valor de

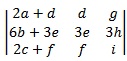
será

(1,0) 6 - 

Considere as funções f : R → R tal que f(x) = −x² + 11x −10 e g : R → R tal que g(x) = x² − 9x + 18.

Sendo h a função definida por h(x) = log(f (x) /g(x)), o domínio de h será

(1,0) 7 - 

Sendo

o valor real de A + B será

(1,0) 8 - 

Na figura abaixo, estão representadas as funções reais ƒ(x)= 3^0,5x e g(x)= log₃ (x⁄2)

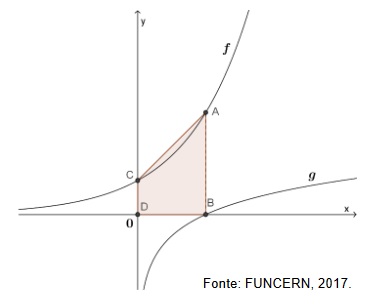
Considerando que os pontos A e B possuem mesma abscissa, o valor da área do quadrilátero ABCD é

(1,0) 9 - 

Um ponto P pertence ao gráfico da função real f(x) = (x − 1)². Esse ponto está situado no primeiro quadrante, e a distância até o vértice da parábola é igual a 2√5.

Com base nessas informações, a soma da ordenada com a abscissa do ponto P será

(1,0) 10 - 

Sobre progressões aritméticas, é correto afirmar:

(1,0) 11 - 

Jailton saiu caminhando para o trabalho a uma velocidade constante de 10 km/h. Seu irmão percebeu que ele esqueceu o celular e, como conhecia o trajeto, resolveu ir de bicicleta entregá-lo. O irmão saiu 18 minutos após a saída de Jailton e andou a uma velocidade constante de 25 km/h.

A distância que o irmão percorreu até encontrar Jailton foi de

(1,0) 12 - 

A função ƒ(x) = x³⁄6 + 1⁄2x tem como representação gráfica a figura abaixo.

O comprimento do arco definido no intervalo de abscissa 1 < x < 2, é de

(1,0) 13 - 

Uma empresa sustentável projeta uma nova embalagem em formato cilíndrico, fabricada em determinado tipo de papelão de alta resistência e com capacidade para 0,4 litros de líquido.

Se a quantidade de material a ser utilizada com a lateral e as bases deve ser a menor possível, a medida interna do raio da base dessa embalagem, em cm, será

(1,0) 14 - 

Uma fazenda tem o formato retangular e está dividida em quatro lotes, conforme se apresenta na figura abaixo.

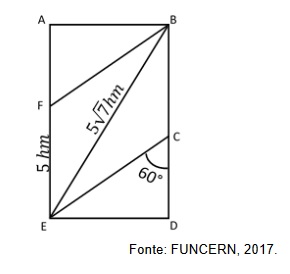
Considerando que os segmentos BF e CE são paralelos e que o segmento EF mede 5hm, o valor mais próximo da área dessa fazenda é

(1,0) 15 - 

Seja

, a soma dos possíveis valores de x é igual a