Simulado Geometria Espacial para o Enem | ENEM
SIMULADO GEOMETRIA ESPACIAL PARA O ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Geometria Espacial, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Simulado Geometria Espacial para o Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Geometria Espacial, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #204587
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com 10 cm de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfuração de base circular (C).
O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (I) 3,8 cm; (II) 4,7 cm; (III) 5,6 cm; (IV) 7,2 cm e (V) 9,4 cm.

Considere 1,4 e 1,7 como aproximações para √2 e √3, respectivamente.
Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?
- a) I
- b) II
- c) III
- d) IV
- e) V
- #204589
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.

Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
- a) Cilindro, prisma de base pentagonal e pirâmide.
- b) Cone, prisma de base pentagonal e pirâmide.
- c) Cone, tronco de pirâmide e pirâmide.
- d) Cilindro, tronco de pirâmide e prisma.
- e) Cilindro, prisma e tronco de cone.
- #204590
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
- a) 5 cm.
- b) 6 cm.
- c) 12 cm.
- d) 24 cm.
- e) 25 cm.
- #204591
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.
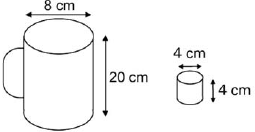
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá
- a) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
- b) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o volume do copo.
- c) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o volume do copo.
- d) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
- e) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o volume do copo.
- #204592
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Uma empresa vende tanques de combustíveis de formato cilíndrico, em três tamanhos, com medidas indicadas nas figuras. O preço do tanque é diretamente proporcional à medida da área da superfície lateral do tanque. O dono de um posto de combustível deseja encomendar um tanque com menor custo por metro cúbico de capacidade de armazenamento.

Qual dos tanques deverá ser escolhido pelo dono do posto? (Considere π ≅ 3)
- a) I, pela relação área/capacidade de armazenamento de 1⁄3
- b) I, pela relação área/capacidade de armazenamento de 4⁄3
- c) II, pela relação área/capacidade de armazenamento de 3⁄4
- d) III, pela relação área/capacidade de armazenamento de 2⁄3
- e) III, pela relação área/capacidade de armazenamento de 7⁄12
- #204593
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
Para construir uma manilha de esgoto, um cilindro com 2 m de diâmetro e 4 m de altura (de espessura desprezível), foi envolvido homogeneamente por uma camada de concreto, contendo 20 cm de espessura.
Supondo que cada metro cúbico de concreto custe R$ 10,00 e tomando 3,1 como valor aproximado de π então o preço dessa manilha é igual a
- a) R$ 230,40.
- b) R$ 124,00.
- c) R$ 104,16.
- d) R$ 54,56.
- e) R$ 49,60.
- #204594
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.

O volume de madeira utilizado na confecção desse objeto foi de
- a) 12 cm3 .
- b) 64 cm3 .
- c) 96 cm3 .
- d) 1 216 cm3 .
- e) 1 728 cm3 .
- #204601
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Os três recipientes da figura têm formas diferentes, mas a mesma altura e o mesmo diâmetro da boca. Neles são colocados líquido até a metade de sua altura, conforme indicado nas figuras. Representando por

o volume de líquido em cada um dos recipientes, tem-se

- a)

- b)
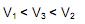
- c)

- d)

- e)

- #204608
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.

Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
- a) 156 cm3 .
- b) 189 cm3 .
- c) 192 cm3 .
- d) 216 cm3 .
- e) 540 cm3 .
- #204611
- Banca
- . Bancas Diversas
- Matéria
- Geometria Espacial
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Um artesão construiu peças de artesanato interceptando uma pirâmide de base quadrada com um plano. Após fazer um estudo das diferentes peças que poderia obter, ele concluiu que uma delas poderia ter uma das faces pentagonal.
Qual dos argumentos a seguir justifica a conclusão do artesão?
- a) Uma pirâmide de base quadrada tem 4 arestas laterais e a interseção de um plano com a pirâmide intercepta suas arestas laterais. Assim, esses pontos formam um polígono de 4 lados.
- b) Uma pirâmide de base quadrada tem 4 faces triangulares e, quando um plano intercepta essa pirâmide, divide cada face em um triângulo e um trapézio. Logo, um dos polígonos tem 4 lados.
- c) Uma pirâmide de base quadrada tem 5 faces e a interseção de uma face com um plano é um segmento de reta. Assim, se o plano interceptar todas as faces, o polígono obtido nessa interseção tem 5 lados.
- d) O número de lados de qualquer polígono obtido como interseção de uma pirâmide com um plano é igual ao número de faces da pirâmide. Como a pirâmide tem 5 faces, o polígono tem 5 lados.
- e) O número de lados de qualquer polígono obtido interceptando-se uma pirâmide por um plano é igual ao número de arestas laterais da pirâmide. Como a pirâmide tem 4 arestas laterais, o polígono tem 4 lados.

