Simulado ENEM | Matemática | ENEM
SIMULADO ENEM | MATEMÁTICA
INSTRUÇÕES DESTE SIMULADO
OBJETIVOS DO SIMULADO
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores concursos públicos do País, através de simulado para ENEM, prova do ENEM e/ou questões do ENEM.
PÚBLICO ALVO DO SIMULADO
Alunos que almejam sua aprovação no ENEM. Que desejam tirar excelentes notas na prova do ENEM deste ano.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões do ENEM e da banca INEP. Estas questões são especificamente para o Aluno ENEM , contendo Matemática que foram extraídas de provas anteriores, portanto este simulado contém os gabaritos oficiais destas provas do ENEM.
ESTATÍSTICA DO SIMULADO
O simulado ENEM | Matemática contém um total de 20 questões com um tempo estimado de 60 minutos para sua realização. O assunto abordado é diversificado para que você possa realmente simular como esta seus conhecimentos.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES. Venha participar deste Ranking do ENEM e saia na frente de todos. Veja sua nota e sua colocação e saiba se esta preparado para conseguir sua aprovação.
Bons Estudos! Simulado para o ENEM é aqui!
- #86335
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
No tanque de um certo carro de passeio cabem até 50 L de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível. Ao sair para uma viagem de 600 km o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do medidor, conforme figura a seguir.

Como o motorista conhece o percurso, sabe que existem, até a chegada a seu destino, cinco postos de abastecimento de combustível, localizados a 150 km, 187 km, 450 km, 500 km e 570 km do ponto de partida.
Qual a máxima distância, em quilômetro, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?
- a) 570
- b) 500
- c) 450
- d) 187
- e) 150
- #86340
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
Densidade absoluta (d) é a razão entre a massa de um corpo e o volume por ele ocupado. Um professor propôs à sua turma que os alunos analisassem a densidade de três corpos: dA, dB, dC. Os alunos verificaram que o corpo A possuía 1,5 vez a massa do corpo B e esse, por sua vez, tinha 3/4 da massa do corpo C. Observaram, ainda, que o volume do corpo A era o mesmo do corpo B e 20% maior do que o volume do corpo C.
Após a análise, os alunos ordenaram corretamente as densidades desses corpos da seguinte maneira
- a) dB < dA < dC
- b) dB = dA < dC
- c) dC < dB = dA
- d) dB < dC < dA
- e) dC < dB < dA
- #86347
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m x 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo que os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará.
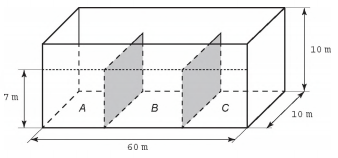
Suponha que ocorra um desastre quando o petroleiro se encontra com sua carga máxima: ele sofre um acidente que ocasiona um furo no fundo do compartimento C.
Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias.
Após o fim do vazamento, o volume de petróleo derramado terá sido de
- a) 1,4 X 103m3
- b) 1,8 X 103m3
- c) 2,0 X 103m3
- d) 3,2 X 103m3
- e) 6,0 X 103m3
- #86349
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Uma liga metálica sai do forno a uma temperatura de 3 000 °C e diminui 1% de sua temperatura a cada 30 min.
Use 0,477 como aproximação para log10(3) e 1,041 como aproximação para log10(11).
O tempo decorrido, em hora, até que a liga atinja 30 °C é mais próximo de
- a) 22.
- b) 50.
- c) 100.
- d) 200.
- e) 400.
- #86350
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Um posto de saúde registrou a quantidade de vacinas aplicadas contra febre amarela nos últimos cinco meses:
• 1° mês: 21;
• 2° mês: 22;
• 3° mês: 25;
• 4° mês: 31;
• 5° mês: 21.
No início do primeiro mês, esse posto de saúde tinha 228 vacinas contra febre amarela em estoque. A política de reposição do estoque prevê a aquisição de novas vacinas, no início do sexto mês, de tal forma que a quantidade inicial em estoque para os próximos meses seja igual a 12 vezes a média das quantidades mensais dessas vacinas aplicadas nos últimos cinco meses.
Para atender essas condições, a quantidade de vacinas contra febre amarela que o posto de saúde deve adquirir no início do sexto mês é
- a) 156.
- b) 180.
- c) 192 .
- d) 264.
- e) 288.
- #86354
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
Um dos grandes desafios do Brasil é o gerenciamento I dos seus recursos naturais, sobretudo os recursos hídricos. Existe uma demanda crescente por água e o risco de racionamento não pode ser descartado. O nível de água de um reservatório foi monitorado por um período, sendo o resultado mostrado no gráfico. Suponha que essa tendência linear observada no monitoramento se prolongue pelos próximos meses.
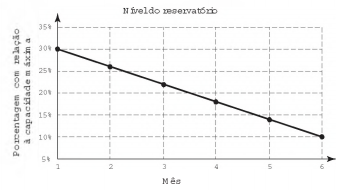
- a) 2 meses e meio.
- b) 3 meses e meio.
- c) 1 mês e meio.
- d) 4 meses.
- e) 1 mês.
- #86359
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo, caso contrário, ele será despedido. O quadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso.

- a) 26
- b) 29
- c) 30
- d) 31
- e) 35
- #86361
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Num campeonato de futebol de 2012, um time sagrou-se campeão com um total de 77 pontos (P) em 38 jogos, tendo 22 vitórias (V), 11 empates (E) e 5 derrotas (D). No critério adotado para esse ano, somente as vitórias e empates têm pontuações positivas e inteiras. As derrotas têm valor zero e o valor de cada vitória é maior que o valor de cada empate.
Um torcedor, considerando a fórmula da soma de pontos injusta, propôs aos organizadores do campeonato que, para o ano de 2013, o time derrotado em cada partida perca 2 pontos, privilegiando os times que perdem menos ao longo do campeonato. Cada vitória e cada empate continuariam com a mesma pontuação de 2012.
Qual a expressão que fornece a quantidade de pontos (P), em função do número de vitórias (V), do número de empates (E) e do número de derrotas (D), no sistema de pontuação proposto pelo torcedor para o ano de 2013?
- a) P = 3V + E
- b) P = 3V - 2D
- c) P = 3V + E - D
- d) P = 3V + E - 2D
- e) P = 3V + E + 2D
- #86367
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
Um técnico precisa consertar o termostato do aparelho de ar-condicionado de um escritório, que está desregulado. A temperatura T, em graus Celsius, no escritório, varia de acordo com a função T (h) = A + B sen ![]()
sendo h o tempo, medido em horas, a partir da meia-noite (0 ? h ? 24) e A e B os parâmetros que o técnico precisa regular. Os funcionários do escritório pediram que a temperatura máxima fosse 26°C, a mínima 18°C, e que durante a tarde a temperatura fosse menor do que durante a manhã.
Quais devem ser os valores de A e de B para que o pedido dos funcionários seja atendido?
- a) A = 18 e B = 8
- b) A = 22 e B = - 4
- c) A = 22 e B = 4
- d) A = 26 e B = - 8
- e) A = 26 e B = 8
- #86375
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Uma empresa que embala seus produtos em caixas de papelão, na forma de hexaedro regular, deseja que seu logotipo seja impresso nas faces opostas pintadas de cinza, conforme a figura:
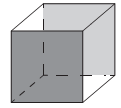
A gráfica que fará as impressões dos logotipos apresentou as seguintes planificadas:
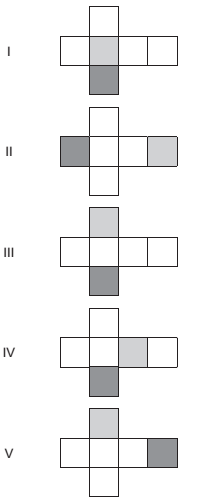
Que opção sugerida pela gráfica atende ao desejo da empresa?
- a) I
- b) II
- c) III
- d) IV
- e) V
- #86376
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 11 -
Uma fábrica brasileira de exportação de peixes vende para o exterior atum em conserva, em dois tipos de latas cilíndricas: uma de altura igual a 4 cm e raio 6 cm, e outra de altura desconhecida e raio de 3 cm, respectivamente, conforme figura. Sabe-se que a medida do volume da lata que possui raio maior, V1, é 1,6 vezes a medida do volume da lata que possui raio menor, V2.
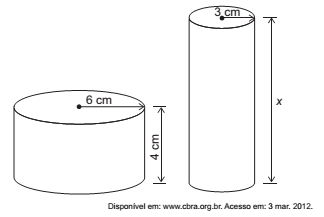
A medida da altura desconhecida vale
- a) 8 cm.
- b) 10 cm.
- c) 16 cm.
- d) 20 cm.
- e) 40 cm.
- #86377
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 12 -
Atendendo à encomenda de um mecânico, um soldador terá de juntar duas barras de metais diferentes. A solda utilizada tem espessura de 18 milímetros, conforme ilustrado na figura.
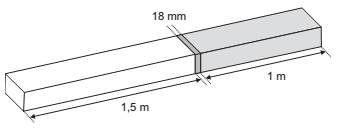
Qual o comprimento, em metros, da peça resultante após a soldagem?
- a) 2,0230
- b) 2,2300
- c) 2,5018
- d) 2,5180
- e) 2,6800
- #86378
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 13 -
Um artesão fabrica vários tipos de potes cilíndricos. Mostrou a um cliente um pote de raio de base a e altura b. Esse cliente, por sua vez, quer comprar um pote com o dobro do volume do pote apresentado. O artesão diz que possui potes com as seguintes dimensões:
• Pote I: raio a e altura 2b
• Pote II: raio 2a e altura b
• Pote III: raio 2a e altura 2b
• Pote IV: raio 4a e altura b
• Pote V: raio 4a e altura 2b
O pote que satisfaz a condição imposta pelo cliente é o
- a) I.
- b) II.
- c) III.
- d) IV.
- e) V.
- #86379
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 14 -
A bandeira de um estado é formada por cinco faixas, A, B, C, D e E, dispostas conforme a figura.
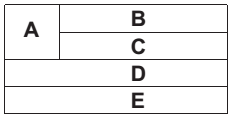
Deseja-se pintar cada faixa com uma das cores verde, azul ou amarelo, de tal forma que faixas adjacentes não sejam pintadas com a mesma cor.
O cálculo do número de possibilidades distintas de se pintar essa bandeira, com a exigência acima, é
- a) 1 x 2 x 1 x 1 x 2.
- b) 3 x 2 x 1 x 1 x 2
- c) 3 x 2 x 1 x 1 x 3.
- d) 3 x 2 x 1 x 2 x 2.
- e) 3 x 2 x 2 x 2 x 2.
- #86380
- Banca
- INEP
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 15 -
O modelo predador-presa foi proposto de forma independente por Alfred J. Lotka, em 1925, e Vito Volterra, em 1926. Esse modelo descreve a interação entre duas espécies, sendo que uma delas dispõe de alimentos para sobreviver (presa) e a outra se alimenta da primeira (predador). Considere que o gráfico representa uma interação predador-presa, relacionando a população do predador com a população da sua presa ao longo dos anos.
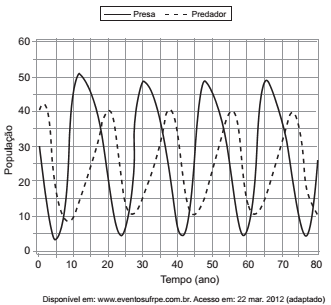
De acordo com o gráfico, nos primeiros quarenta anos, quantas vezes a população do predador se igualou à da presa?
- a) 2
- b) 3
- c) 4
- d) 5
- e) 9

