Simulado ENEM | Matemática | ENEM

(1,0) 1 - 

O gráfico mostra a variação da extensão média de gelo marítimo, em milhões de quilômetros quadrados, comparando dados dos anos 1995, 1998, 2000, 2005 e 2007. Os dados correspondem aos meses de junho a setembro. O Ártico começa a recobrar o gelo quando termina o verão, em meados de setembro. O gelo do mar atua como o sistema de resfriamento da Terra, refletindo quase toda a luz solar de volta ao espaço. Águas de oceanos escuros, por sua vez, absorvem a luz solar e reforçam o aquecimento do Ártico, ocasionando derretimento crescente do gelo.

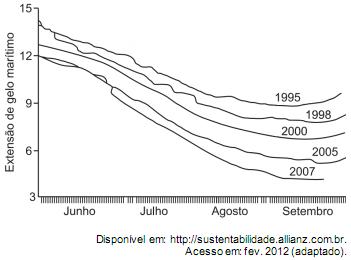
Com base no gráfico e nas informações do texto, é possível inferir que houve maior aquecimento global em

(1,0) 2 - 

Um caminhão precisa recolher o lixo das ruas de um certo bairro. Por questões econômicas e ambientais, a empresa IMJ, responsável pela coleta, planeja as rotas de recolhimento, de modo que o caminhão percorra a menor distância possível, passando em cada rua exatamente uma vez, entrando e saindo de cada ponto. Quando isso não é possível, busca-se repetir o menor número possível de ruas na rota. Na figura, temos um esquema no qual os pontos representam esquinas, e as linhas representam as ruas.

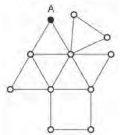
Considere que cada rua mede 150 m de comprimento e que a rota do caminhão comece e termine no ponto A, passando por todas as ruas do esquema.

A empresa conseguiu encontrar a melhor rota de recolhimento de lixo, na qual o caminhão percorre uma distância igual a

(1,0) 3 - 

O gráfico faz uma comparação entre os crescimentos das ações da Vale e da Ibovespa de janeiro a abril de 2010.

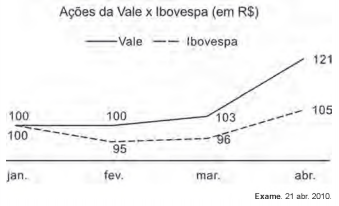
De acordo com as informações do gráfico, o crescimento das ações da Vale e da Ibovespa no período de janeiro a abril de 2010 foram, respectivamente, de

(1,0) 4 - 

élia é uma confeiteira renomada na pequena cidade onde mora. Herdou de sua avó uma receita de brigadeiro que faz o maior sucesso. Os ingredientes da receita enchem sempre uma panela, de forma cilíndrica, com 40 cm de altura e 30 cm de diâmetro. Para inovar e atrair mais clientes, em vez de vender os brigadeiros na forma de "bolinhas", Célia tem feito brigadeiros em forma de cones. Para isso, utiliza forminhas cônicas de 5 cm de altura e raio da base de 1,5 cm.

A cada receita produzida, a quantidade de cones de brigadeiro que Célia consegue obter é

(1,0) 5 - 

Numa sementeira, cinco canteiros quadrados serão preparados para plantar, em cada um, dois tipos de sementes: A e B. Os canteiros estão representados segundo as figuras:

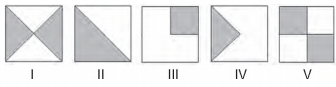
Suponha que cada canteiro tem 1 m2 de área e que nas regiões sombreadas de cada canteiro serão plantadas as sementes do tipo A. Qual o total da área, em m2, reservada para as sementes do tipo B?

(1,0) 6 - 

Fabiana Murer garante mais uma medalha de ouro na Noruega. A atleta brasileira saltou 4,60 m na etapa da Diamond League e terminou em primeiro lugar na disputa. Ela ainda é detentora da melhor marca do ano. Ao final da prova, a classificação dos quatro melhores resultados foi:

1° lugar: Fabiana Murer (BRA) - 4,60 m

2° lugar: Aleksandra Kiryashiva (RUS) - 4,50 m

3° lugar: Anna Rogowska (POL) - 4,40 m

4° lugar: Monika Pyrek (POL) - 4,30 m

Disponível em: http://www.globoesporte.globo.com. Acesso em: 24 jun. 2011 (adaptado).

A diferença entre as marcas da 1a e da 4a colocadas pode ser comparada com a altura de um animal adulto. Que animal é esse?

(1,0) 7 - 

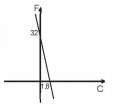
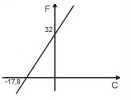
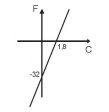
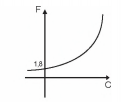
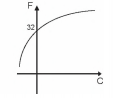
No Brasil, costumamos medir temperaturas utilizando a escala Celsius. Os países de língua inglesa utilizam a escala Farenheit. A relação entre essas duas escalas é dada pela expressão F = C x 1,8 + 32, em que F representa a medida da temperatura na escala Farenheit e C a medida da temperatura na escala Celsius.

O gráfico que representa a relação entre essas duas grandezas é

(1,0) 8 - 

Um administrador de um campo de futebol deseja recobri-lo com um tipo de grama que, em condições normais, cresce de acordo com o gráfico a seguir.

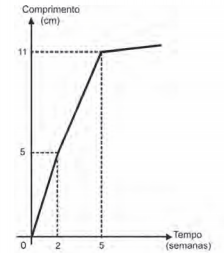
Ele precisa ter o campo pronto no dia 11 de junho de 2012, e o comprimento mínimo da grama nesse dia deve ser igual a 7 cm.

Supondo-se que o crescimento da grama se dê em condições normais, a grama deve ser plantada, no máximo, até o dia

(1,0) 9 - 

Os medicamentos, imediatamente após a ingestão, começam a ser metabolizados pelo organismo, o que faz com que sua concentração no sangue diminua gradualmente, num processo denominado decaimento. Denomina-se meia-vida de uma substância o tempo necessário para que o teor dessa substância no sangue se reduza à metade do valor inicial.

Considere a situação em que um médico prescreveu a um paciente uma dosagem de 800 mg de um medicamento cuja meia-vida é 6 horas, com recomendação de tomar um comprimido a cada 12 horas, durante 3 dias. Para esse medicamento, considera-se superdosagem um teor superior a 1 520 mg, o que causa riscos de intoxicação.

Apressado em recuperar-se a tempo de ir a uma festa, o paciente sugeriu ao médico que mudasse a prescrição para 6 em 6 horas, imaginando que, assim, reduziria o tempo de tratamento. O médico contra-argumentou, informando ao paciente que, caso antecipasse as doses, correria o risco de estar intoxicado em

(1,0) 10 - 

Em 2009, o Estado de São Paulo perdeu 3 205,7 hectares de sua cobertura vegetal, área 30% menor que a desmatada em 2008, segundo balanço do projeto ambiental estratégico "Desmatamento Zero", divulgado pela Secretaria do Meio Ambiente (SMA).

São Paulo reduz área desmatada. Boletim Agência FAPESP.

Disponível em: http://www.agencia.fapesp.br. Acesso em: 26 abr. 2010.

Um hectare é uma unidade de medida de área equivalente a 100 ares. Um are, por sua vez, é equivalente a 100 m2. Logo, a área 3 205,7 hectares corresponde a

(1,0) 11 - 

Por falta de tratamentos simples, mais de 1 bilhão de pessoas pobres no mundo acordam doentes todos os dias. Entre essas doenças está a ancilostomose, que aflige 600 milhões de pessoas e causa anemia severa e desnutrição proteica. Para fornecer tratamento a essas pessoas, estima-se um gasto anual de cinquenta centavos de dólar por paciente.

HORTEZ, P. J. Um plano para derrotar Doenças Tropicais Negligenciadas. Scientific American Brasil. Ano 8, no 33 (adaptado).

Uma organização está disposta a lançar uma campanha internacional a fim de obter recursos suficientes para cobrir o tratamento das pessoas com ancilostomose por um ano. Segundo seu planejamento, estima-se um valor médio de US$ 3,00 por doador.

De acordo com o planejamento dessa organização, para arrecadar o total de recursos necessários para cobrir o tratamento das pessoas com ancilostomose, por um ano, o número mínimo de contribuintes necessários é de

(1,0) 12 - 

Pedro ganhou R$ 360 000,00 em uma loteria federal e resolveu dividir integralmente o prêmio entre os seus três filhos, Ana, Renato e Carlos, de forma que cada um receba uma quantia que seja inversamente proporcional às suas idades.

Sabendo que Ana tem 4 anos, Renato, 5 anos e Carlos, 20 anos, eles receberão, respectivamente,

(1,0) 13 - 

Um programador visual deseja modificar uma imagem, aumentando seu comprimento e mantendo sua largura. As figuras 1 e 2 representam, respectivamente, a imagem original e a transformada pela duplicação do comprimento.

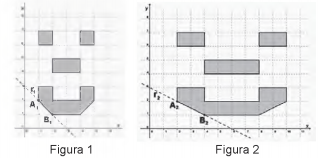
Para modelar todas as possibilidades de transformação no comprimento dessa imagem, o programador precisa descobrir os padrões de todas as retas que contêm os segmentos que contornam os olhos, o nariz e a boca e, em seguida, elaborar o programa.

No exemplo anterior, o segmento A1B1 da figura 1, contido na reta r1, transformou-se no segmento A2B2 da figura 2, contido na reta r2.

Suponha que, mantendo constante a largura da imagem, seu comprimento seja multiplicado por n, sendo n um número inteiro e positivo, e que, dessa forma, a reta r1sofra as mesmas transformações. Nessas condições, o segmento AnBn estará contido na reta rn .

A equação algébrica que descreve rn, no plano cartesiano, é

(1,0) 14 - 

Atualmente existem muitos aplicativos de fazendas virtuais que, apesar de críticas, possuem uma enorme quantidade de usuários. Embora apresentem algumas diferenças de funcionamento, as fazendas virtuais possuem a mesma concepção: cada vez que o usuário cuida de sua fazenda ou da de seus amigos, ganha pontos, e, quanto mais pontos acumula, maior é seu nível de experiência.

Em um aplicativo de fazenda virtual, o usuário precisa de 1 000 pontos para atingir o nível 1. Acumulando mais 1 200 pontos, atinge o nível 2; acumulando mais 1 400 pontos, atinge o nível 3 e assim por diante, sempre com esse padrão.

Um usuário que está no nível 15 de experiência acumulou

(1,0) 15 - 

Uma enquete, realizada em março de 2010, perguntava aos internautas se eles acreditavam que as atividades humanas provocam o aquecimento global. Eram três as alternativas possíveis e 279 internautas responderam à enquete, como mostra o gráfico.

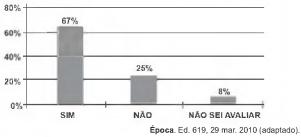
Analisando os dados do gráfico, quantos internautas responderam “NÃO” à enquete?