Simulado Binômio de Newton | CONCURSO
Simulado Binômio de Newton
Se você irá prestar algum concurso que cobre a matéria de Binômio de Newton não pode deixar de praticar com nossos simulados grátis.
Vejam todos os simulados Binômio de Newton
São milhares de simulados para concurso disponível para você praticar e conseguir a tão sonhada aprovação em Concurso Público.
Este Simulado Binômio de Newton foi elaborado da seguinte forma:
- Categoria: Concurso
- Instituição:
Diversas - Cargo: Diversos
- Matéria: Binômio de Newton
- Assuntos do Simulado: Diversos
- Banca Organizadora: Diversas
- Quantidade de Questões: 5
- Tempo do Simulado: 15 minutos
Vejam outros Simulado Binômio de Newton
REGRA DO SIMULADO
Para realizar este simulado, que é gratuito, você apenas precisara criar no botão Iniciar logo abaixo e realizar um breve cadastro (apenas apelido e e-mail) para que assim você possa participar do Ranking do Simulado.
Por falar em Ranking, todos os nossos simulados contém um ranking, assim você saberá como esta indo em seus estudos e ainda poderá comparar sua nota com a dos seus concorrentes.
Aproveitem estes simulados Binômio de Newton e saiam na frente em seus estudos.
Questões Binômio de Newton
Caso você ainda não se sinta preparado para realizar um simulado, você poderá treinar em nossas questões de concursos, principalmente as questões de Binômio de Newton, que também são grátis. Clique Aqui!
Vejam todos os simulados Binômio de Newton
Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z
- #241568
- Banca
- . Bancas Diversas
- Matéria
- Binômio de Newton
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
No desenvolvimento de (x + 2 )n . x3 , o coeficiente de xn+1 é igual a:
- a) n3 + 1
- b) n + 2
- c) 2n(n - 1)
- d) n2 (n + 1)
- e) n2 - 3n + 2
- #241569
- Banca
- . Bancas Diversas
- Matéria
- Binômio de Newton
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
O termo independente de x no desenvolvimento do binômio de Newton
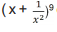
é:
- a) 72.
- b) 78.
- c) 80.
- d) 84.
- e) 92.
- #241570
- Banca
- . Bancas Diversas
- Matéria
- Binômio de Newton
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
No desenvolvimento de P(x) = (ax2 − 2bx + c + 1)2 , obtenha o valor do coeficiente de maior grau sendo a = 2, b = -1 e c = 5.
- a) 2
- b) 4
- c) 8
- d) 12
- e) 16
- #241571
- Banca
- . Bancas Diversas
- Matéria
- Binômio de Newton
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Considere que o número de termos do desenvolvimento de um binômio de Newton seja igual a z + 7. Então, é correto afirmar que o expoente desse binômio será igual a
- a) z + 2.
- b) z + 4.
- c) z + 6.
- d) z + 8.
- e) 8.
- #241572
- Banca
- . Bancas Diversas
- Matéria
- Binômio de Newton
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Considere as seguintes afirmações abaixo:
I. Se A é um evento e Ac seu complementar, então P(Ac ) = 1 − P(A).
II. Consideremos 3 eventos, A, B e C do mesmo espaço amostral Ω. Diremos que, A, B e C são independentes, se:
− P(A ∩ B) = P(A) ⋅ P(B)
− P(A ∩ C) = P(A) ⋅ P(C)
− P(B ∩ C) = P(B) ⋅ P(C)
− P(A ∩ B ∩ C) = P(A) ⋅ P(B) ⋅ P(C)
III. A distribuição Pk = ( n k ) ∙pk ∙ qn−k é chamada binomial, pois cada probabilidade Pk é dada pelo termo geral do binômio de Newton (p + q)n , de exatamente K sucessos nos n ensaios.
Assinale o item correto.
- a) Somente I está correto.
- b) Somente II está correto.
- c) Somente III está correto.
- d) Somente I e II estão corretos.
- e) Todas as afirmações estão corretas.

