Simulado Álgebra Linear para o Enem | ENEM
SIMULADO ÁLGEBRA LINEAR PARA O ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Álgebra Linear, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Simulado Álgebra Linear para o Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Álgebra Linear, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #204549
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
A Transferência Eletrônica Disponível (TED) é uma transação financeira de valores entre diferentes bancos. Um economista decide analisar os valores enviados por meio de TEDs entre cinco bancos (1,2, 3, 4 e 5) durante um mês. Para isso, ele dispõe esses valores em uma matriz A = [aij], em que 1 ≤ i ≤ 5 e 1 ≤ j ≤ 5, e o elemento aij corresponde ao total proveniente das operações feitas via TED, em milhão de real, transferidos do banco i para o banco j durante o mês. Observe que os elementos aij = 0, uma vez que TED é uma transferência entre bancos distintos. Esta é a matriz obtida para essa análise:
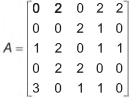
Com base nessas informações, o banco que transferiu a maior quantia via TED é o banco
- a) 1.
- b) 2.
- c) 3.
- d) 4.
- e) 5.
- #204552
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
Um professor aplica, durante os cinco dias úteis de uma semana, testes com quatro questões de múltipla escolha a cinco alunos. Os resultados foram representados na matriz.

Nessa matriz os elementos das linhas de 1 a 5 representam as quantidades de questões acertadas pelos alunos Ana, Bruno, Carlos, Denis e Érica, respectivamente, enquanto que as colunas de 1 a 5 indicam os dias da semana, de segunda-feira a sexta-feira, respectivamente, em que os testes foram aplicados.
O teste que apresentou maior quantidade de acertos foi o aplicado na
- a) segunda-feira.
- b) terça-feira.
- c) quarta-feira.
- d) quinta-feira.
- e) sexta-feira.
- #204555
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Uma construtora, pretendendo investir na construção de imóveis em uma metrópole com cinco grandes regiões, fez uma pesquisa sobre a quantidade de famílias que mudaram de uma região para outra, de modo a determinar qual região foi o destino do maior fluxo de famílias, sem levar em consideração o número de famílias que deixaram a região. Os valores da pesquisa estão dispostos em uma matriz A = [aij], i, j ∈ {1,2, 3, 4, 5}, em que o elemento aij corresponde ao total de famílias (em dezena) que se mudaram da região i para a região j durante um certo período, e o elemento aii considerado nulo, uma vez que somente são consideradas mudanças entre regiões distintas. A seguir, está apresentada a matriz com os dados da pesquisa.
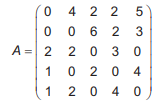
Qual região foi selecionada para o investimento da construtora?
- a) 1
- b) 2
- c) 3
- d) 4
- e) 5
- #204556
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Uma construtora, pretendendo investir na construção de imóveis em uma metrópole com cinco grandes regiões, fez uma pesquisa sobre a quantidade de famílias que mudaram de uma região para outra, de modo a determinar qual região foi o destino do maior fluxo de famílias, sem levar em consideração o número de famílias que deixaram a região. Os valores da pesquisa estão dispostos em uma matriz A = [aij], i, j ∈ {1,2,3,4,5}, em que o elemento aij corresponde ao total de famílias (em dezena) que se mudaram da região i para a região j durante um certo período, e o elemento a é considerado nulo, uma vez que somente são consideradas mudanças entre regiões distintas. A seguir, está apresentada a matriz com os dados da pesquisa.
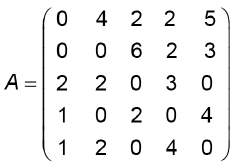
Qual região foi selecionada para o investimento da construtora?
- a) 1
- b) 2
- c) 3
- d) 4
- e) 5
- #204557
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Uma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas.
Devido a urna demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada.
A quantidade X, de placas do novo modelo, em cada nova caixa será igual a:
- a) N/9
- b) N/6
- c) N/3
- d) 3N
- e) 9N
- #204558
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
Médicos alertam sobre a importância de educar as crianças para terem hábitos alimentares saudáveis. Por exemplo, analisando-se uma bolacha com recheio de chocolate (25 g) e um pé de alface (25 g), observam-se as seguintes quantidades de nutrientes, respectivamente:
• carboidratos: 15 g e 0,5 g;
• proteínas: 1,9 g e 0,5 g.
Disponível em: http://veja.abril.com.br. Acesso em: 27 abr. 2010 (adaptado).
Considerando as informações apresentadas, qual deve ser o número de pés de alface consumidos para se obter a mesma quantidade de carboidratos de uma bolacha?
- a) 50
- b) 30
- c) 14
- d) 8
- e) 7
- #204561
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
Durante uma festa de colégio, um grupo de alunos organizou uma rifa. Oitenta alunos faltaram à festa e não participaram da rifa. Entre os que compareceram, alguns compraram três bilhetes, 45 compraram 2 bilhetes, e muitos compraram apenas um. O total de alunos que comprou um único bilhete era 20% do número total de bilhetes vendidos, e o total de bilhetes vendidos excedeu em 33 o número total de alunos do colégio.
Quantos alunos compraram somente um bilhete?
- a) 34
- b) 42
- c) 47
- d) 48
- e) 79
- #204562
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Em uma corrida de regularidade, cada corredor recebe um mapa com o trajeto a ser seguido e uma tabela indicando intervalos de tempo e distâncias entre postos de averiguação. O objetivo dos competidores é passar por cada um dos postos de averiguação o mais próximo possível do tempo estabelecido na tabela. Suponha que o tempo previsto para percorrer a distância entre dois postos de verificação consecutivos seja sempre de 5 min 15 s, e que um corredor obteve os seguintes tempos nos quatro primeiros postos.
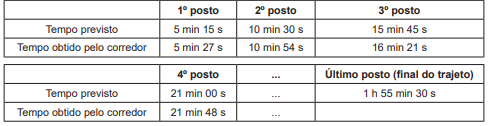
Caso esse corredor consiga manter o mesmo ritmo, seu tempo total de corrida será
- a) 1 h 55 min 42 s.
- b) 1 h 56 min 30 s.
- c) 1 h 59 min 54 s.
- d) 2 h 05 min 09 s.
- e) 2 h 05 min 21 s.
- #204563
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
As coordenadas usualmente utilizadas na localização de um ponto sobre a superfície terrestre são a latitude e a longitude. Para tal, considera-se que a Terra tem a forma de uma esfera.
Um meridiano é uma circunferência sobre a superfície da Terra que passa pelos polos Norte e Sul, representados na figura por PN e PS. O comprimento da semicircunferência que une os pontos PN e PS tem comprimento igual a 20 016 km. A linha do Equador também é uma circunferência sobre a superfície da Terra, com raio igual ao da Terra, sendo que o plano que a contém é perpendicular ao que contém qualquer meridiano.
Seja P um ponto na superfície da Terra, C o centro da Terra e o segmento
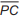
um raio, conforme mostra a figura. Seja ϕ o ângulo que o segmento
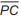
faz com o plano que contém a linha do Equador. A medida em graus de ϕ é a medida da latitude de P.
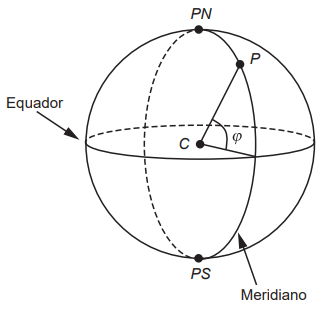
Suponha que a partir da linha do Equador um navio viaja subindo em direção ao Polo Norte, percorrendo um meridiano, até um ponto P com 30 graus de latitude.
Quantos quilômetros são percorridos pelo navio?
- a) 1 668
- b) 3 336
- c) 5 004
- d) 6 672
- e) 10 008
- #204569
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz 4x4, e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuíam o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir.
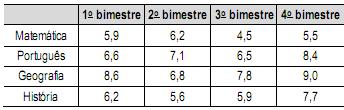
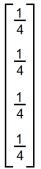
Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela por
- a)
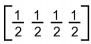
- b)
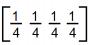
- c)

- d)

- e)