Simulado Algarismo Romano | ENEM
Simulado Algarismo Romano
Se você irá prestar algum concurso que cobre a matéria de Algarismo Romano não pode deixar de praticar com nossos simulados grátis.
Vejam todos os simulados Algarismo Romano
São milhares de simulados para concurso disponível para você praticar e conseguir a tão sonhada aprovação em Concurso Público.
Este Simulado Algarismo Romano foi elaborado da seguinte forma:
- Categoria: Enem
- Instituição:
Enem - Cargo: Aluno Enem
- Matéria: Algarismo Romano
- Assuntos do Simulado: Diversas
- Banca Organizadora: Inep
- Quantidade de Questões: 1
- Tempo do Simulado: 3 minutos
Vejam outros Simulado Algarismo Romano
REGRA DO SIMULADO
Para realizar este simulado, que é gratuito, você apenas precisara criar no botão Iniciar logo abaixo e realizar um breve cadastro (apenas apelido e e-mail) para que assim você possa participar do Ranking do Simulado.
Por falar em Ranking, todos os nossos simulados contém um ranking, assim você saberá como esta indo em seus estudos e ainda poderá comparar sua nota com a dos seus concorrentes.
Aproveitem estes simulados Algarismo Romano e saiam na frente em seus estudos.
Questões Algarismo Romano
Caso você ainda não se sinta preparado para realizar um simulado, você poderá treinar em nossas questões de concursos, principalmente as questões de Algarismo Romano, que também são grátis. Clique Aqui!
Vejam todos os simulados Algarismo Romano
Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z
- #225747
- Banca
- INEP
- Matéria
- Algarismo Romano
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
Suponha que, na escultura do artista Emanoel Araújo, mostrada na figura a seguir, todos os prismas numerados em algarismos romanos são retos, com bases triangulares, e que as faces laterais do poliedro II são perpendiculares à sua própria face superior, que, por sua vez, é um triângulo congruente ao triângulo base dos prismas. Além disso, considere que os prismas I e III são perpendiculares ao prisma IV e ao poliedro II.
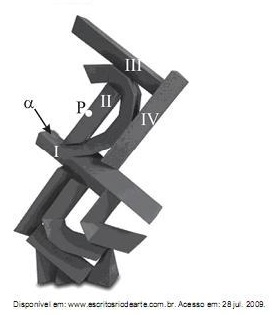
Imagine um plano paralelo à face a do prisma I, mas que passe pelo ponto P pertencente à aresta do poliedro II, indicado na figura. A interseção desse plano imaginário com a escultura contém
- a) dois triângulos congruentes com lados correspondentes paralelos.
- b) dois retângulos congruentes e com lados correspondentes paralelos.
- c) dois trapézios congruentes com lados correspondentes perpendiculares.
- d) dois paralelogramos congruentes com lados correspondentes paralelos.
- e) dois quadriláteros congruentes com lados correspondentes perpendiculares.

