Questões de Álgebra para o Enem | ENEM
QUESTÕES DE ÁLGEBRA PARA O ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Álgebra, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Questões de Álgebra para o Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Álgebra, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #198088
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas da tabela formavam uma matriz 4x4, e que poderia calcular as médias anuais dessas disciplinas usando produto de matrizes. Todas as provas possuíam o mesmo peso, e a tabela que ele conseguiu é mostrada a seguir.
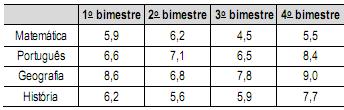
Para obter essas médias, ele multiplicou a matriz obtida a partir da tabela por
- a)
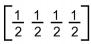
- b)
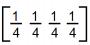
- c)

- d)

- e)
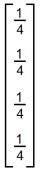
- #198089
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
O gráfico mostra a variação da extensão média de gelo marítimo, em milhões de quilômetros quadrados, comparando dados dos anos 1995, 1998, 2000, 2005 e 2007. Os dados correspondem aos meses de junho a setembro. O Ártico começa a recobrar o gelo quando termina o verão, em meados de setembro. O gelo do mar atua como o sistema de resfriamento da Terra, refletindo quase toda a luz solar de volta ao espaço. Águas de oceanos escuros, por sua vez, absorvem a luz solar e reforçam o aquecimento do Ártico, ocasionando derretimento crescente do gelo.
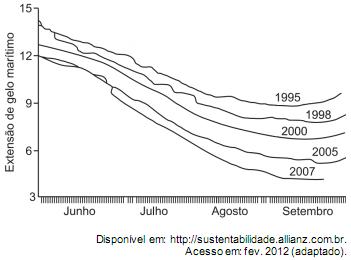
Com base no gráfico e nas informações do texto, é possível inferir que houve maior aquecimento global em
- a) 1995.
- b) 1998.
- c) 2000.
- d) 2005.
- e) 2007.
- #198090
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Certo vendedor tem seu salário mensal calculado da seguinte maneira: ele ganha um valor fixo de R$ 750,00, mais uma comissão de R$ 3,00 para cada produto vendido. Caso ele venda mais de 100 produtos, sua comissão passa a ser de R$ 9,00 para cada produto vendido, a partir do 101o produto vendido.
Com essas informações, o gráfico que melhor representa a relação entre salário e o número de produtos vendidos é
- a)
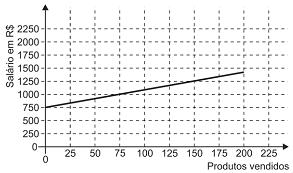
- b)
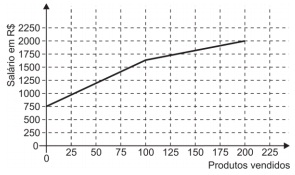
- c)
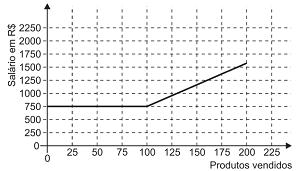
- d)
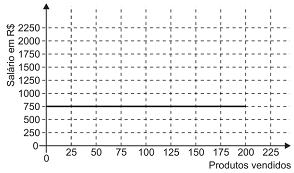
- e)
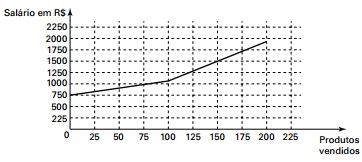
- #198091
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Em um laboratório, cientistas observaram o crescimento de uma população de bactérias submetida a uma dieta magra em fósforo, com generosas porções de arsênico. Descobriu-se que o número de bactérias dessa população, após t horas de observação, poderia ser modelado pela função exponencial N(t) = N0ekt, em que N0 é o número de bactérias no instante do início da observação (t = 0) e representa uma constante real maior que 1, e k é uma constante real positiva.
Sabe-se que, após uma hora de observação, o número de bactérias foi triplicado. Cinco horas após o início da observação, o número de bactérias, em relação ao número inicial dessa cultura, foi
- a) 3N0
- b) 15N0
- c) 243N
- d) 360N0
- e) 729N0
- #198092
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Recíproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e a altura, uma variável de dimensões lineares. As fórmulas que determinam esses índices são:

Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m2 , então ela possui RIP igual a
- a) 0,4 cm/kg1/3 .
- b) 2,5 cm/kg1/3 .
- c) 8 cm/kg1/3 .
- d) 20 cm/kg1/3 .
- e) 40 cm/kg1/3 .
- #198093
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um
salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado. Disponível em: www.cbat.org.br (adaptado).
Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m.
Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre
- a) 4,0 m e 5,0 m.
- b) 5,0 m e 6,0 m.
- c) 6,0 m e 7,0 m.
- d) 7,0 m e 8,0 m.
- e) 8,0 m e 9,0 m.
- #198098
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
- #198103
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
O Índice de Massa Corporal (IMC) é largamente utilizado há cerca de 200 anos, mas esse cálculo representa muito mais a corpulência que a adiposidade, uma vez que indivíduos musculosos e obesos podem apresentar o mesmo IMC. Uma nova pesquisa aponta o Índice de Adiposidade Corporal (IAC) como uma alternativa mais fidedigna para quantificar a gordura corporal, utilizando a medida do quadril e a altura. A figura mostra como calcular essas medidas, sabendo- se que, em mulheres, a adiposidade normal está entre 19% e 26%.
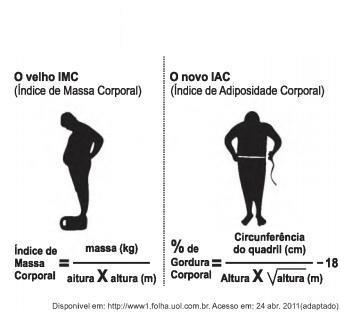
Uma jovem com IMC = 20 kg/m2, 100 cm de circunferência dos quadris e 60 kg de massa corpórea resolveu averiguar seu IAC. Para se enquadrar aos níveis de normalidade de gordura corporal, a atitude adequada que essa jovem deve ter diante da nova medida é
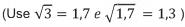
- a) reduzir seu excesso de gordura em cerca de 1%.
- b) reduzir seu excesso de gordura em cerca de 27%.
- c) manter seus níveis atuais de gordura.
- d) aumentar seu nível de gordura em cerca de 1%.
- e) aumentar seu nível de gordura em cerca de 27%.
- #198104
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ 100 000,00 por km construído (n), acrescidos de um valor fixo de R$ 350 000,00, enquanto a segunda cobrou R$ 120 000,00 por km construído (n), acrescidos de um valor fixo de R$ 150 000,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada.
Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas?
- a) 100n+ 350 = 120n+150
- b) 100n+ 150 = 120n+350
- c) 100(n + 350) = 120(n + 150)
- d) 100(n + 350 000) = 120(n + 150 000)
- e) 350(n + 100 000) = 150(n + 120 000)
- #198105
- Banca
- . Bancas Diversas
- Matéria
- Álgebra
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Um técnico em refrigeração precisa revisar todos os pontos de saída de ar de um escritório com várias salas.
Na imagem apresentada, cada ponto indicado por uma letra é a saída do ar, e os segmentos são as tubulações.
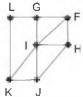
Iniciando a revisão pelo ponto K e terminando em F, sem passar mais de uma vez por cada ponto, o caminho será passando pelos pontos
- a) K, I e F.
- b) K, J, I, G, L e F.
- c) K, L, G, I, J, H e F.
- d) K, J, H, I, G, L e F.
- e) K, L, G, I, H, J e F.


