Questões de Álgebra Linear para Concursos Diversos | CONCURSO
📚 Simulado Álgebra Linear gratuito | cód.9014
Domine Álgebra Linear com questões focadas no estilo das bancas. Bora treinar? 🎯
🔗 Veja mais simulados de Álgebra Linear
🎯 São milhares de simulados para concurso disponíveis para você praticar Álgebra Linear e conquistar a tão sonhada aprovação em Concurso Público.
🧪 Este Simulado de Álgebra Linear foi elaborado da seguinte forma:
- 📌 Categoria: Concurso
- 🏛️ Instituição: . Concursos Diversos
- 👔 Cargo: . Cargos Diversos
- 📚 Matéria: Álgebra Linear
- 🤩 Assuntos do Simulado:
- 🏢 Banca Organizadora: . Bancas Diversas
- ❓ Quantidade de Questões: 20
- ⏱️ Tempo do Simulado: 60 minutos
⚙️ REGRA DO SIMULADO
Este simulado é gratuito 🆓. Basta clicar no botão iniciar abaixo e preencher um breve cadastro para participar do nosso ranking.
📊 No ranking você compara sua nota com outros candidatos e acompanha sua evolução nos estudos.
🚀 Aproveite este simulado de Álgebra Linear e saia na frente na sua preparação!
📚 Questões de Álgebra Linear
Se ainda não estiver pronto para fazer o simulado, treine antes com nossas questões de concursos:
🎥 Vídeo Aula
Confira vídeo aulas no YouTube sobre a disciplina Álgebra Linear. Estude com conteúdo gratuito e atualizado.
Assistir vídeo aula sobre Álgebra Linear
📚 Apostila
Encontre apostilas completas e materiais atualizados de Álgebra Linear.
Ver apostilas de Álgebra Linear
🍀 Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z ✅
- #133036
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 16 -
Considere o sistema:
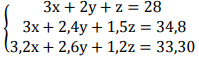
Quanto ao sistema dado, anteriormente, dos itens a seguir, a única afirmação verdadeira é:
- a) O sistema apresentado não é linear;
- b) x = 3,y = 4,5 e z = 10 é solução do sistema;
- c) O sistema é indeterminado e admite infinitas soluções;
- d) O sistema é impossível, pois, não admite solução.
- #133037
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 17 -
Qual a solução do sistema de equações de 1º grau
?
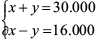
- a) 5.10³ e 25.10³
- b) 7.10³ e 23.10³
- c) 15.10³ e 17.10³
- d) 12.10³ e 18.10³
- #133038
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 18 -
Resolva, em R, a equação
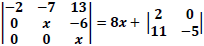
e, assinale a alternativa CORRETA acerca do conjunto solução:
- a) S = {−1, 5}
- b) S = {1}
- c) S = {−5}
- d) S = {1, −5}
- #133039
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 19 -
Considere as proposições:
I. det(A) = det(AT ), para toda matriz A quadrada de ordem n.
III. det(In) = 1, em que In é a matriz identidade de ordem n.
IV. Se A e B são matrizes quadradas de ordem n, então é sempre verdade que det(A + B) = det(A) + det(B)
Assinale a alternativa em que apresenta a quantidade de proposição(ões) CORRETA(S):
- a) 4
- b) 0
- c) 1
- d) 2
- #133040
- Banca
- . Bancas Diversas
- Matéria
- Álgebra Linear
- Concurso
- . Concursos Diversos
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 20 -
Sobre as matrizes Amxn e Bpxq é correto afirmar que existe a operação:
- a) A + B, se n = p
- b) B – A, se n = p
- c) A · B, se m = q
- d) B · A, se m = q