Prova Probabilidade para o Enem | ENEM
PROVA PROBABILIDADE PARA O ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Probabilidade, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Prova Probabilidade para o Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Probabilidade, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #189934
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
A figura I abaixo mostra um esquema das principais vias que interligam a cidade A com a cidade B. Cada número indicado na figura II representa a possibilidade de pegar um engarrafamento quando se passa na via indicada. Assim, há uma probabilidade de 30% de se pegar engarrafamento no deslocamento do ponto C ao o ponto B, passando pela estrada E4, e de 50%, quando se passa por E3. Essas probabilidades são independentes umas das outras.
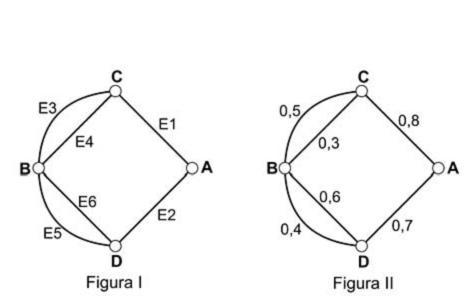
Paula deseja se deslocar da cidade A para a cidade B usando exatamente duas das vias indicadas, percorrendo um trajeto com a menor probabilidade de engarrafamento possível.
O melhor trajeto para Paula é
- a) E1E3.
- b) E1E4.
- c) E2E4.
- d) E2E5.
- e) E2E6.
- #189942
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
O diretor de um colégio leu numa revista que os pés das mulheres estavam aumentando. Há alguns anos, a média do tamanho dos calçados das mulheres era de 35,5 e, hoje, é de 37,0. Embora não fosse uma informação científica, ele ficou curioso e fez uma pesquisa com as funcionárias do seu colégio, obtendo o quadro a seguir:
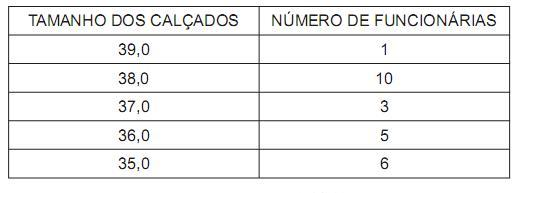
Escolhendo uma funcionária ao acaso e sabendo que ela tem calçado maior que 36,0, a probabilidade de ela calçar 38,0 é
- a) 1/3
- b) 1/5
- c) 2/5
- d) 5/7
- e) 5/14
- #189949
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Um aluno de uma escola será escolhido por sorteio para representá-la em uma certa atividade. A escola tem dois turnos. No diurno há 300 alunos, distribuídos em 10 turmas de 30 alunos. No noturno há 240 alunos, distribuídos em 6 turmas de 40 alunos.
Em vez do sorteio direto envolvendo os 540 alunos, foram propostos dois outros métodos de sorteio.
Método I : escolher ao acaso um dos turnos (por exemplo, lançando uma moeda) e, a seguir, sortear um dos alunos do turno escolhido.
Método II: escolher ao acaso uma das 16 turmas (por exemplo, colocando um papel com o número de cada turma em uma urna e sorteando uma delas) e, a seguir, sortear um dos alunos dessa turma. Sobre os métodos I e II de sorteio é correto afirmar:
- a) em ambos os métodos, todos os alunos têm a mesma chance de serem sorteados.
- b) no método I, todos os alunos têm a mesma chance de serem sorteados, mas, no método II a chance de um aluno do diurno ser sorteado é maior que a de um aluno do noturno.
- c) no método II, todos os alunos têm a mesma chance de serem sorteados, mas, no método I, a chance de um aluno do diurno ser sorteado é maior que a de um aluno do noturno.
- d) no método I, a chance de um aluno do noturno ser sorteado é maior do que a de um aluno do diurno, enquanto no método II ocorre o contrário.
- e) em ambos os métodos, a chance de um aluno do diurno ser sorteado é maior do que a de um aluno do noturno.
- #189958
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
As 23 ex-alunas de uma turma que completou o Ensino Médio há 10 anos se encontraram em uma reunião comemorativa. Várias delas haviam se casado e tido filhos. A distribuição das mulheres, de acordo com a quantidade de filhos, é mostrada no gráfico abaixo.
Um prêmio foi sorteado entre todos os filhos dessas ex-alunas. A probabilidade de que a criança premiada tenha sido um(a) filho(a) único(a) é
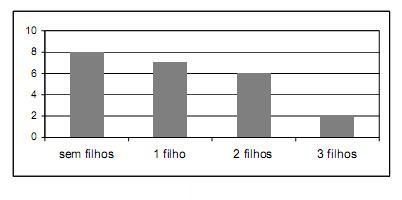
- a) 1/3.
- b) 1/4.
- c) 7/15.
- d) 7/23.
- e) 7/25.
- #189971
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
A queima de cana aumenta a concentração de dióxido de carbono e de material particulado na atmosfera, causa alteração do clima e contribui para o aumento de doenças respiratórias. A tabela abaixo apresenta números relativos a pacientes internados em um hospital no período da queima da cana.

Escolhendo-se aleatoriamente um paciente internado nesse hospital por problemas respiratórios causados pelas queimadas, a probabilidade de que ele seja uma criança é igual a
- a) 0,26, o que sugere a necessidade de implementação de medidas que reforcem a atenção ao idoso internado com problemas respiratórios.
- b) 0,50, o que comprova ser de grau médio a gravidade dos problemas respiratórios que atingem a população nas regiões das queimadas.
- c) 0,63, o que mostra que nenhum aspecto relativo à saúde infantil pode ser negligenciado.
- d) 0,67, o que indica a necessidade de campanhas de conscientização que objetivem a eliminação das queimadas.
- e) 0,75, o que sugere a necessidade de que, em áreas atingidas pelos efeitos das queimadas, o atendimento hospitalar no setor de pediatria seja reforçado.
- #189983
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
O controle de qualidade de uma empresa fabricante de telefones celulares aponta que a probabilidade de um aparelho de determinado modelo apresentar defeito de fabricação é de 0,2%. Se uma loja acaba de vender 4 aparelhos desse modelo para um cliente, qual é a probabilidade de esse cliente sair da loja com exatamente dois aparelhos defeituosos?
- a) 2 × (0,2%) 4 .
- b) 4 × (0,2%) 2 .
- c) 6 × (0,2%) 2× (99,8%) 2 .
- d) 4 × (0,2%).
- e) 6 × (0,2%) × (99,8%).
- #189985
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
A população brasileira sabe, pelo menos intuitivamente, que a probabilidade de acertar as seis dezenas da mega sena não é zero, mas é quase. Mesmo assim, milhões de pessoas são atraídas por essa loteria, especialmente quando o prêmio se acumula em valores altos. Até junho de 2009, cada aposta de seis dezenas, pertencentes ao conjunto {01, 02, 03, ..., 59, 60}, custava R$ 1,50.
Disponível em: www.caixa.gov.br. Acesso em: 7 jul. 2009.
Considere que uma pessoa decida apostar exatamente R$ 126,00 e que esteja mais interessada em acertar apenas cinco das seis dezenas da mega sena, justamente pela dificuldade desta última. Nesse caso, é melhor que essa pessoa faça 84 apostas de seis dezenas diferentes, que não tenham cinco números em comum, do que uma única aposta com nove dezenas, porque a probabilidade de acertar a quina no segundo caso em relação ao primeiro é, aproximadamente,
- a) 1 1/2 vez menor.
- b) 2 1/2 vezes menor.
- c) 4 vezes menor.
- d) 9 vezes menor.
- e) 14 vezes menor.
- #189988
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Um médico está estudando um novo medicamento que combate um tipo de câncer em estágios avançados. Porém, devido ao forte efeito dos seus componentes, a cada dose administrada há uma chance de 10% de que o paciente sofra algum dos efeitos colaterais observados no estudo, tais como dores de cabeça, vômitos ou mesmo agravamento dos sintomas da doença. O médico oferece tratamentos compostos por 3, 4, 6, 8 ou 10 doses do medicamento, de acordo com o risco que o paciente pretende assumir.
Se um paciente considera aceitável um risco de até 35% de chances de que ocorra algum dos efeitos colaterais durante o tratamento, qual é o maior número admissível de doses para esse paciente?
- a) 3 doses.
- b) 4 doses.
- c) 6 doses.
- d) 8 doses.
- e) 10 doses.
- #189993
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
Rafael mora no Centro de uma cidade e decidiu se mudar, por recomendações médicas, para uma das regiões: Rural, Comercial, Residencial Urbano ou Residencial Suburbano. A principal recomendação médica foi com as temperaturas das “ilhas de calor” da região, que deveriam ser inferiores a 31 °C. Tais temperaturas são apresentadas no gráfico:
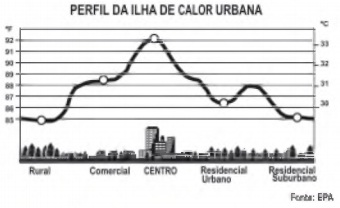
Escolhendo, aleatoriamente, uma das outras regiões para morar, a probabilidade de ele escolher uma região que seja adequada às recomendações médicas é
- a) 1/5
- b) 1/4
- c) 2/5
- d) 3/5
- e) 3/4
- #189999
- Banca
- . Bancas Diversas
- Matéria
- Probabilidade
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Em um jogo disputado em uma mesa de sinuca, há 16 bolas: 1 branca e 15 coloridas, as quais, de acordo com a coloração, valem de 1 a 15 pontos (um valor para cada bola colorida).
O jogador acerta o taco na bola branca de forma que esta acerte as outras, com o objetivo de acertar duas das quinze bolas em quaisquer caçapas. Os valores dessas duas bolas são somados e devem resultar em um valor escolhido pelo jogador antes do início da jogada.
Arthur, Bernardo e Caio escolhem os números 12, 17 e 22 como sendo resultados de suas respectivas somas.
Com essa escolha, quem tem a maior probabilidade de ganhar o jogo é
- a) Arthur, pois a soma que escolheu é a menor.
- b) Bernardo, pois há 7 possibilidades de compor a soma escolhida por ele, contra 4 possibilidades para a escolha de Arthur e 4 possibilidades para a escolha de Caio.
- c) Bernardo, pois há 7 possibilidades de compor a soma escolhida por ele, contra 5 possibilidades para a escolha de Arthur e 4 possibilidades para a escolha de Caio.
- d) Caio, pois há 10 possibilidades de compor a soma escolhida por ele, contra 5 possibilidades para a escolha de Arthur e 8 possibilidades para a escolha de Bernardo.
- e) Caio, pois a soma que escolheu é a maior.

