Prova Matemática Enem | ENEM
PROVA MATEMÁTICA ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Matemática, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Prova Matemática Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Matemática, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #191968
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
O jogo-da-velha é um jogo popular, originado na Inglaterra. O nome “velha” surgiu do fato de esse jogo ser praticado, à época em que foi criado, por senhoras idosas que tinham dificuldades de visão e não conseguiam mais bordar. Esse jogo consiste na disputa de dois adversários que, em um tabuleiro 3×3, devem conseguir alinhar verticalmente, horizontalmente ou na diagonal, 3 peças de formato idêntico. Cada jogador, após escolher o formato da peça com a qual irá jogar, coloca uma peça por vez, em qualquer casa do tabuleiro, e passa a vez para o adversário. Vence o primeiro que alinhar 3 peças.

- a) uma só maneira.
- b) duas maneiras distintas.
- c) três maneiras distintas.
- d) quatro maneiras distintas.
- e) cinco maneiras distintas.
- #191969
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
O tangram é um jogo oriental antigo, uma espécie de quebra-cabeça, constituído de sete peças: 5 triângulos retângulos e isósceles, 1 paralelogramo e 1 quadrado. Essas peças são obtidas recortando-se um quadrado de acordo com o esquema da figura 1. Utilizando-se todas as sete peças, é possível representar uma grande diversidade de formas, como as exemplificadas nas figuras 2 e 3. B

Se o lado AB do hexágono mostrado na figura 2 mede 2 cm, então a área da figura 3, que representa uma “casinha”, é igual a
- a) 4 cm2 .
- b) 8 cm2 .
- c) 12 cm2 .
- d) 14 cm2 .
- e) 16 cm2 .
- #191970
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -

- a) carroça – semana
- b) carro – dia
- c) caminhada – hora
- d) bicicleta – minuto
- e) avião – segundo
- #191971
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Fractal (do latim fractus, fração, quebrado) — objeto que pode ser dividido em partes que possuem semelhança com o objeto inicial. A geometria fractal, criada no século XX, estuda as propriedades e o comportamento dos fractais — objetos geométricos formados por repetições de padrões similares.
O triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. comece com um triângulo equilátero (figura 1);
2. construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias;
3. posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2;
4. repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
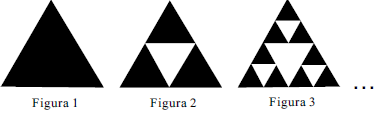
De acordo com o procedimento descrito, a figura 4 da seqüência apresentada acima é
- a)

- b)

- c)

- d)

- e)

- #191972
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
A contagem de bois
Em cada parada ou pouso, para jantar ou dormir, os bois são contados, tanto na chegada quanto na saída. Nesses lugares, há sempre um potreiro, ou seja, determinada área de pasto cercada de arame, ou mangueira, quando a cerca é de madeira. Na porteira de entrada do potreiro, rente à cerca, os peões formam a seringa ou funil, para afinar a fila, e então os bois vão entrando aos poucos na área cercada. Do lado interno, o condutor vai contando; em frente a ele, está o marcador, peão que marca as reses. O condutor conta 50 cabeças e grita: — Talha! O marcador, com o auxílio dos dedos das mãos, vai marcando as talhas. Cada dedo da mão direita corresponde a 1 talha, e da mão esquerda, a 5 talhas. Quando entra o último boi, o marcador diz: — Vinte e cinco talhas! E o condutor completa: — E dezoito cabeças. Isso significa 1.268 bois.
Boiada, comitivas e seus peões. In: O Estado de São Paulo, ano VI, ed. 63, 21/12/1952 (com adaptações).
Para contar os 1.268 bois de acordo com o processo descrito acima, o marcador utilizou
- a) 20 vezes todos os dedos da mão esquerda.
- b) 20 vezes todos os dedos da mão direita.
- c) todos os dedos da mão direita apenas uma vez.
- d) todos os dedos da mão esquerda apenas uma vez.
- e) 5 vezes todos os dedos da mão esquerda e 5 vezes todos os dedos da mão direita.
- #191973
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -

- a) a quantidade de água economizada foi de 4,5 m3 .
- b) a altura do nível da água que sobrou no reservatório, no final do dia, foi igual a 60 cm.
- c) a quantidade de água economizada seria suficiente para abastecer, no máximo, 90 casas cujo consumo diário fosse de 450 litros.
- d) os moradores dessas casas economizariam mais de R$ 200,00, se o custo de 1 m3 de água para o consumidor fosse igual a R$ 2,50.
- e) um reservatório de mesma forma e altura, mas com raio da base 10% menor que o representado, teria água suficiente para abastecer todas as casas.
- #191974
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
Suponha que o universo tenha 15 bilhões de anos de idade e que toda a sua história seja distribuída ao longo de 1 ano — o calendário cósmico —, de modo que cada segundo corresponda a 475 anos reais e, assim, 24 dias do calendário cósmico equivaleriam a cerca de 1 bilhão de anos reais. Suponha, ainda, que o universo comece em 1.º de janeiro a zero hora no calendário cósmico e o tempo presente esteja em 31 de dezembro às 23 h 59 min 59,99 s. A escala abaixo traz o período em que ocorreram alguns eventos importantes nesse calendário.
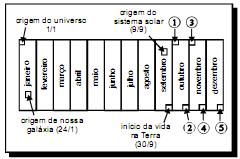

- a) 1.
- b) 2.
- c) 3.
- d) 4.
- e) 5.
- #191975
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -

Ao ler esse texto em uma sala de aula, uma professora fez uma suposição de que o diâmetro do olho humano mede aproximadamente 2,1 cm.
Qual a razão entre o diâmetro aproximado do olho humano, suposto pela professora, e o diâmetro do espelho primário do telescópio citado?
- a) 1 : 20
- b) 1 : 100
- c) 1 : 200
- d) 1 : 1 000
- e) 1 : 2 000
- #191976
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura.
Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
- a) 5 cm.
- b) 6 cm.
- c) 12 cm.
- d) 24 cm.
- e) 25 cm.
- #191977
- Banca
- . Bancas Diversas
- Matéria
- Matemática
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
A loja Telas & Molduras cobra 20 reais por metro quadrado de tela, 15 reais por metro linear de moldura, mais uma taxa fixa de entrega de 10 reais.
Uma artista plástica precisa encomendar telas e molduras a essa loja, suficientes para 8 quadros retangulares (25 cm × 50 cm). Em seguida, fez uma segunda encomenda, mas agora para 8 quadros retangulares (50 cm × 100 cm). O valor da segunda encomenda será
- a) o dobro do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
- b) maior do que o valor da primeira encomenda, mas não o dobro.
- c) a metade do valor da primeira encomenda, porque a altura e a largura dos quadros dobraram.
- d) menor do que o valor da primeira encomenda, mas não a metade.
- e) igual ao valor da primeira encomenda, porque o custo de entrega será o mesmo.

