Prova Funções para o Enem | ENEM
PROVA FUNÇÕES PARA O ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Funções, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Prova Funções para o Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Funções, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #190492
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função do tipo P(t) = A + Bcos(kt) em que A, B e K são constantes reais positivas e t representa a variável tempo, medida em segundo. Considere que um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões máximas.
Ao analisar um caso específico, o cientista obteve os dados:

A função P(t) obtida, por este cientista, ao analisar o caso específico foi
- a) P(t) = 99 + 2 1 cos(3πt)
- b) P(t) = 78 + 42cos(3πt)
- c) P(t) = 99 + 21 cos(2πt)
- d) P(t) = 99 + 21 cos(t)
- e) P(t) = 78 + 42cos(t)
- #190493
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
Um técnico precisa consertar o termostato do aparelho de ar-condicionado de um escritório, que está desregulado. A temperatura T, em graus Celsius, no escritório, varia de acordo com a função T (h) = A + B sen
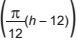
, sendo h o tempo, medido em horas, a partir da meia-noite (0 ≤ h ≤ 24) e A e B os parâmetros que o técnico precisa regular. Os funcionários do escritório pediram que a temperatura máxima fosse 26°C, a mínima 18°C, e que durante a tarde a temperatura fosse menor do que durante a manhã.
Quais devem ser os valores de A e de B para que o pedido dos funcionários seja atendido?
- a) A = 18 e B = 8
- b) A = 22 e B = - 4
- c) A = 22 e B = 4
- d) A = 26 e B = - 8
- e) A = 26 e B = 8
- #190494
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Uma pessoa usa um programa de computador que descreve o desenho da onda sonora correspondente a um som escolhido. A equação da onda é dada, num sistema de coordenadas cartesianas, por y = a . sen[b(x + c)], em que os parâmetros a, b, c são positivos. O programa permite ao usuário provocar mudanças no som, ao fazer alterações nos valores desses parâmetros. A pessoa deseja tornar o som mais agudo e, para isso, deve diminuir o período da onda.
O(s) único(s) parâmetro(s) que necessita(m) ser alterado(s) é(são)
- a) a.
- b) b.
- c) c.
- d) a e b.
- e) b e c.
- #190495
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:
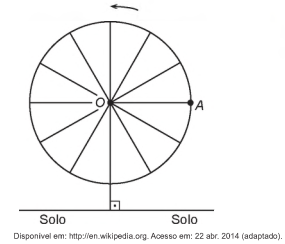
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t.
Após duas voltas completas, f em o seguinte gráfico:
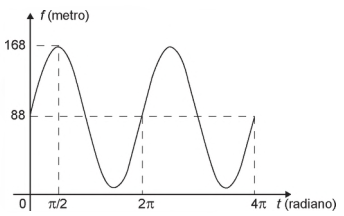
A expressão da função altura é dada por
- a) f(t) = 80sen(t) + 88
- b) f(t) = 80cos(t) + 88
- c) f(t) = 88 cos(t)+168
- d) f(t) = 168sen(t) + 88 cos(t)
- e) f(t) = 88 sen(t)+ 168cos(t)
- #190496
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = ± A cos (ωt) ou P(t) = ± A sen (ωt), em que A > 0 é a amplitude de deslocamento máximo e ω é a frequência, que se relaciona com o período T pela fórmula ω = 2π/T.
Considere a ausência de quaisquer forças dissipativas.
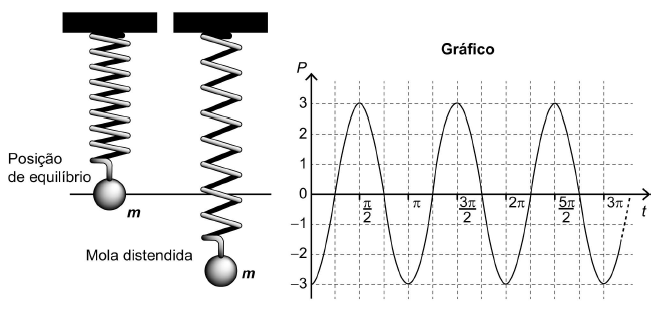
A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é
- a) – 3 sen (2t)
- b) – 3 sen (2t)
- c) 3 cos (2t)
- d) – 6 cos (2t)
- e) 6 sen (2t)
- #190497
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
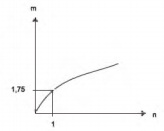
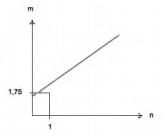
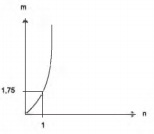
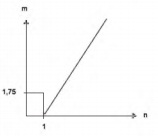
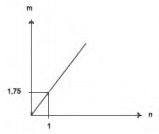
As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção. Considere que, independente da época ou variação de preço, certa fruta custa R$ 1,75 o quilograma.
Dos gráficos a seguir, o que representa o preço m pago em reais pela compra de n quilogramas desse produto é
- a)
- b)
- c)
- d)
- e)
- #190498
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
Em setembro de 1987, Goiânia foi palco do maior acidente radioativo ocorrido no Brasil, quando uma amostra de césio-137, removida de um aparelho de radioterapia abandonado, foi manipulada inadvertidamente por parte da população. A meia-vida de um material radioativo é o tempo necessário para que a massa desse material se reduza à metade. A meia-vida do césio-137 é 30 anos e a quantidade restante de massa de um material radioativo, após t anos, é calculada peta expressão M(t) = A . (2,7)kt , onde A é a massa inicial e k é uma constante negativa.
Considere 0,3 como aproximação para log102.
Qual o tempo necessário, em anos, para que uma quantidade de massa do césio-137 se reduza a 10% da quantidade inicial?
- a) 27
- b) 36
- c) 50
- d) 54
- e) 100
- #190499
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Um engenheiro projetou um automóvel cujos vidros das portas dianteiras foram desenhados de forma que suas bordas superiores fossem representadas pela curva de equação y = log (x), conforme a figura.
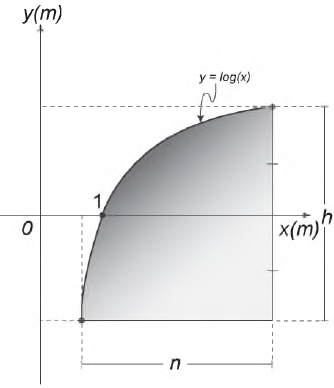
A forma do vidro foi concebida de modo que o eixo x sempre divida ao meio a altura h do vidro e a base do vidro seja paralela ao eixo x. Obedecendo a essas condições, o engenheiro determinou uma expressão que fornece a altura h do vidro em função da medida n de sua base, em metros.
A expressão algébrica que determina a altura do vidro é
- a)
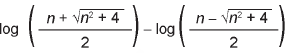
- b)
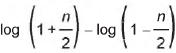
- c)
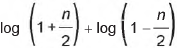
- d)
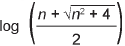
- e)
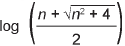
- #190500
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
Em 2011, um terremoto de magnitude 9,0 na escala Richter causou um devastador tsunami no Japão, provocando um alerta na usina nuclear de Fukushima. Em 2013, outro terremoto, de magnitude 7,0 na mesma escala, sacudiu Sichuan (sudoeste da China), deixando centenas de mortos e milhares de feridos. A magnitude de um terremoto na escala Richter pode ser calculada por
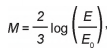
sendo E a energia, em kWh, liberada pelo terremoto e E0 uma constante real positiva. Considere que E1 e E2 representam as energias liberadas nos terremotos ocorridos no Japão e na China, respectivamente.
Disponível em: www.terra.com.br. Acesso em: 15 ago. 2013 (adaptado).
Qual a relação entre E1 e E2?
- a) E1 = E2 + 2
- b) E1 = 102 • E2
- c) E1 = 103 • E2
- d) E1 = 109/7 • E2
- e) E1 = 9/7 • E2
- #190501
- Banca
- . Bancas Diversas
- Matéria
- Funções
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
A Lei de Zipf, batizada com o nome do linguista americano George Zipf, é uma lei empírica que relaciona a frequência (f) de uma palavra em um dado texto com o seu ranking (r). Ela é dada por
f = A/ rB
O ranking da palavra é a sua posição ao ordenar as palavras por ordem de frequência. Ou seja, r = 1 para a palavra mais frequente, r = 2 para a segunda palavra mais frequente e assim sucessivamente, A e B são constantes positivas.
Disponível em: http://klein.sbm.org.br. Acesso em: 12 ago. 2020 (adaptado).
Com base nos valores de X = log (r) e Y = log (f), é possível estimar valores para A e B. No caso hipotético em que a lei é verificada exatamente, a relação entre Y e X é
- a) Y = log (A) - B • X
- b) Y = log(A)/X + log (B)
- c) Y = log (A)/B - X
- d) Y = log (A)/B•X
- e) Y = log(A)/XB

