Prova ENEM - Matemática Enem 6 - Questões e Simulados | ENEM

(1,0) 1 - 

A figura I abaixo mostra um esquema das principais vias que interligam a cidade A com a cidade B. Cada número engarrafamento quando se passa na via indicada. Assim, há uma probabilidade de 30% de se pegar engarrafamento no deslocamento do ponto C ao o ponto B, passando pela estrada E4, e de 50%, quando se passa por E3. Essas probabilidades são independentes umas das outras.

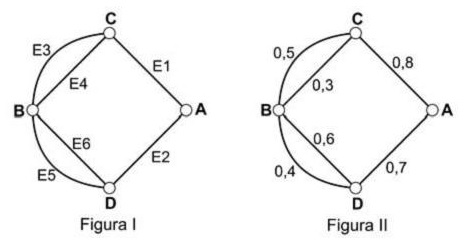
Paula deseja se deslocar da cidade A para a cidade B usando exatamente duas das vias indicadas, percorrendo um trajeto com a menor probabilidade de engarrafamento possível. 

O melhor trajeto para Paula é 

(1,0) 2 - 

O gráfico a seguir apresenta o gasto militar dos Estados Unidos, no período de 1988 a 2006.

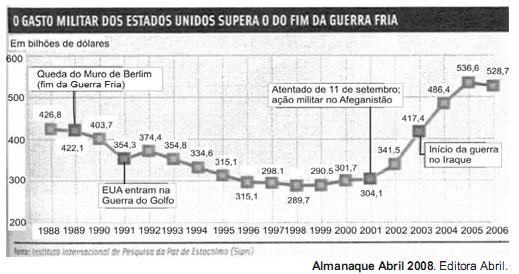
Com base no gráfico, o gasto militar no início da guerra no Iraque foi de

(1,0) 3 - 

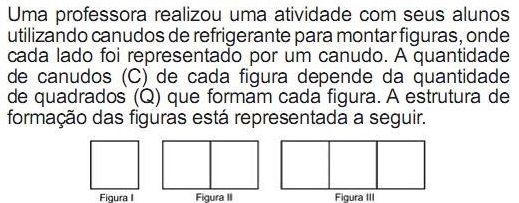
Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?

(1,0) 4 - 

Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.

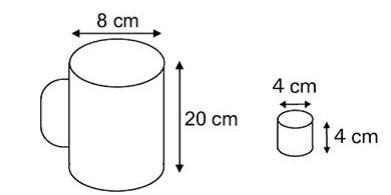
Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá

(1,0) 5 - 

Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor der em função de t seja dado por

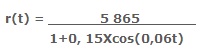
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.

O cientista deveria concluir que, periodicamente, S atinge o valor de

(1,0) 6 - 

Uma empresa vende tanques de combustíveis de formato cilíndrico, em três tamanhos, com medidas indicadas nas figuras. O preço do tanque é diretamente proporcional à medida da área da superfície lateral do tanque. O dono de um posto de combustível deseja encomendar um tanque com menor custo por metro cúbico de capacidade de armazenamento.

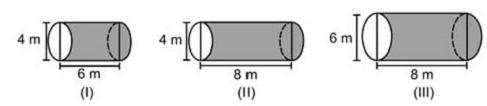
Qual dos tanques deverá ser escolhido pelo dono do posto? (Considere ? ? 3)

(1,0) 7 - 

A figura a seguir é a representação de uma região por meio de curvas de nível, que são curvas fechadas representando a altitude da região, com relação ao nível do mar. As coordenadas estão expressas em graus de acordo com a longitude, no eixo horizontal, e a latitude, no eixo vertical. A escala em tons de cinza desenhada à direita está associada à altitude da região.

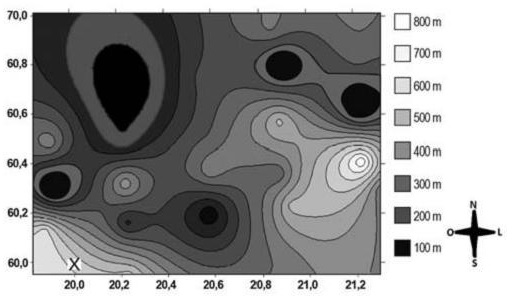
Um pequeno helicóptero usado para reconhecimento sobrevoa a região a partir do ponto X = (20; 60). O helicóptero segue o percurso:

0,8° L ? 0,5° N ? 0,2° O ? 0,1° S ? 0,4° N ? 0,3° L.

Ao final, desce verticalmente até pousar no solo.

De acordo com as orientações, o helicóptero pousou em um local cuja altitude é

(1,0) 8 - 

No manejo sustentável de florestas, é preciso muitas vezes obter o volume da tora que pode ser obtida a partir de uma árvore. Para isso, existe um método prático, em que se mede a circunferência da árvore à altura do peito de um homem (1,30m), conforme indicado na figura. A essa medida denomina-se “rodo” da árvore. O quadro a seguir indica a fórmula para se cubar, ou seja, obter o volume da tora em m³ a partir da medida do rodo e da altura da árvore. 

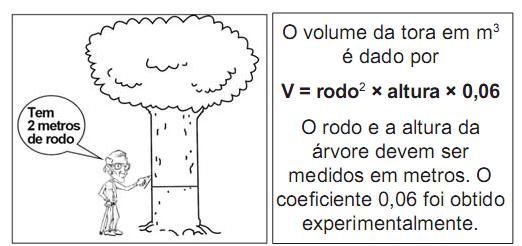
Um técnico em manejo florestal recebeu a missão de cubar, abater e transportar cinco toras de madeira, de duas espécies diferentes, sendo

- 3 toras da espécie I, com 3 m de rodo, 12 m de comprimento e densidade 0,77 toneladas/m³ ;

- 2 toras da espécie II, com 4m de rodo, 10m de comprimento e densidade 0,78 toneladas/m³ .

Após realizar seus cálculos, o técnico solicitou que enviassem caminhões para transportar uma carga de, aproximadamente,

(1,0) 9 - 

Embora o Índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Recíproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e a altura, uma variável de dimensões lineares. As fórmulas que determinam esses índices são:

Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m² , então ela possui RIP igual a

(1,0) 10 - 

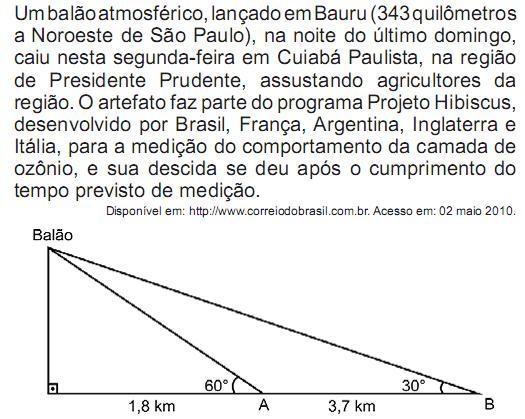
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°. 

Qual a altura aproximada em que se encontrava o balão?