Trigonometria no triangulo retângulo
Trigonometria no triangulo retângulo
Saiba um pouco mais sobre o que são relações métricas no triângulo retângulo!
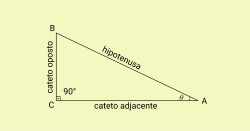
A trigonometria no triângulo retângulo é o estudo sobre os triângulos que possuem um ângulo interno de 90°, chamado de ângulo reto.
Lembre-se que a trigonometria é a ciência responsável pelas relações estabelecidas entre os triângulos. Eles são figuras geométricas planas compostas de três lados e três ângulos internos.
O triângulo chamado equilátero possui os lados com medidas iguais. O isósceles possui dois lados com medidas iguais. Já o escaleno tem os três lados com medidas diferentes.
No tocante aos ângulos dos triângulos, os ângulos internos maiores que 90° são chamados de obtusângulos. Já os ângulos internos menores que 90° são denominados de acutângulos.
Além disso, a soma dos ângulos internos de um triângulo será sempre 180°.
A trigonometria, ao contrário do que se pensa, não é restrita apenas ao triângulo retângulo. Essa área da matemática penetra vários campos da geometria e vai do triângulo acutângulo até às esferas (trigonometria esférica).
VEJA TAMBÉM
- Como resolver a trigonometria no triângulo retângulo?
- Trigonometria no triângulo retângulo exercícios
- Relações métricas no triângulo retângulo
- Calcular ângulo triângulo retângulo
- Trigonometria no triângulo retângulo 9 ano
- Novos Simulados Enem
- Novas Questões Enem
- Provas Anteriores Enem
Como resolver a trigonometria no triângulo retângulo?
O círculo trigonométrico é utilizado para auxiliar nas relações trigonométricas. Acima, podemos encontrar as principais razões, sendo que o eixo vertical corresponde ao seno e o eixo horizontal ao cosseno. Além delas, temos as razões inversas: secante, cossecante e cotangente.
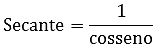
Lê-se um sobre o cosseno.
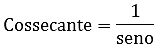
Lê-se um sobre o seno.
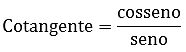
Lê-se cosseno sobre o seno.
Trigonometria no triângulo retângulo exercícios
Um exemplo de questão sobre Trigonometria no triângulo retângulo:
Um avião levanta voo sob um ângulo constante de 20º. Após percorrer 2 000 metros em linha reta, qual será a altura atingida pelo avião, aproximadamente? (Utilize: sem 20º = 0,342; cos 20º = 0,94 e tg 20º = 0,364).
Resposta:
.gif)
.gif)
A altura atingida pelo avião será de 684 metros.
Relações métricas no triângulo retângulo
"As relações métricas são equações que relacionam as medidas dos lados e de alguns outros segmentos de um triângulo retângulo. Para definir essas relações, é importante conhecer esses segmentos.
Elementos do triângulo retângulo
A figura a seguir é um triângulo retângulo ABC, cujo ângulo reto é Â e é cortado pela altura AD:
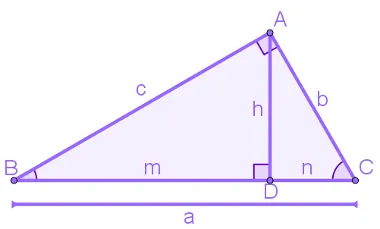
Nesse triângulo, observe que:
- A letra a é a medida da hipotenusa;
- As letras b e c são as medidas dos catetos;
- A letra h é a medida da altura do triângulo retângulo;
- A letra n é a projeção do cateto AC sobre a hipotenusa;
- A letra m é a projeção do cateto BA sobre a hipotenusa.
Calcular ângulo triângulo retângulo
O triângulo retângulo é a forma geométrica que possui um ângulo reto (90°) e dois outros ângulos agudos (menores que 90°). A soma de todos os ângulos internos do triângulo retângulo corresponde a 180°, o que caracteriza como um ângulo raso.
Já seus dois ângulos agudos são conhecidos como complementares, já que a soma dos dois resultará em 90º. O triângulo retângulo é formado por propriedades específicas que mudam de acordo com a posição do ângulo reto.
Trigonometria no triângulo retângulo 9 ano
A Trigonometria está presente em diversas situações cotidianas, sendo considerada um dos mais antigos estudos da humanidade. A relação das medidas de comprimento com os valores dos ângulos surgiu da necessidade de calcular distâncias inacessíveis, sendo os estudos relacionados à Astronomia, Agrimensura e Navegação os primeiros a usarem as relações trigonométricas.
As turmas de 9º ano do Ensino Fundamental possuem nas grades curriculares os estudos introdutórios envolvendo a Trigonometria no Triângulo Retângulo. O professor deve atender essa necessidade, no intuito de preparar o aluno para os conteúdos segmentares do Ensino Médio. Deverão ser trabalhadas as posições relativas entre cateto oposto, cateto adjacente e hipotenusa dos ângulos agudos do triângulo retângulo.

