Teorema de Pitágoras: Explorando Relações no Triângulo Retângulo

O Teorema de Pitágoras desempenha um papel central na matemática, estabelecendo uma relação fundamental entre os lados de um triângulo retângulo. Amplamente utilizado na geometria, esse teorema assume um papel essencial na determinação de dimensões desconhecidas a partir de medidas conhecidas, proporcionando uma compreensão mais aprofundada das propriedades únicas dessa figura geométrica. 

Essa poderosa ferramenta matemática revela-se como uma peça-chave para explorar e compreender as relações espaciais dentro dos triângulos retângulos, tornando-se indispensável em diversas aplicações matemáticas e científicas.

Índice:

1. Contextualização e Enunciado do Teorema
2. Detalhando os Elementos do Teorema
   2.1 a: Hipotenusa
   2.2 b e c: Catetos
3. Aplicações Práticas do Teorema
4. Como surgiu o Teorema de Pitágoras 
5. Teorema de Pitágoras do Dia-a-dia

Contextualização e Enunciado do Teorema

Dentro do vasto universo da geometria, o triângulo retângulo emerge como uma figura peculiar, caracterizada pelo seu ângulo interno de 90°, o qual é conhecido como ângulo reto. É nesse cenário que o Teorema de Pitágoras se destaca, apresentando-se com uma enunciação simples, mas de grande importância: "A hipotenusa ao quadrado é igual à soma dos quadrados dos catetos". Essa expressão matemática estabelece uma relação intrínseca entre os comprimentos dos lados desse triângulo específico, proporcionando uma compreensão única das interações geométricas presentes.

A fórmula associada a esse teorema, expressa como a² = b² + c², consolida essa relação, onde 'a' representa a hipotenusa, enquanto 'b' e 'c' denotam os catetos. Essa equação fundamental desvenda as intricadas conexões existentes em triângulos retângulos, oferecendo uma base sólida para explorar e calcular suas propriedades de maneira precisa e significativa.

Detalhando os Elementos do Teorema

a: Hipotenusa

A hipotenusa, simbolizada por 'a', desempenha um papel fundamental no Teorema de Pitágoras. Este elemento constitui o lado oposto ao ângulo reto em um triângulo retângulo, definindo-se como a face mais extensa da figura. Em termos práticos, compreender a natureza e o comprimento da hipotenusa é essencial, uma vez que seu quadrado, expresso como a², iguala-se à soma dos quadrados dos catetos. Assim, a hipotenusa surge como a peça central dessa equação, conectando os demais elementos do triângulo e permitindo cálculos precisos para determinar dimensões desconhecidas.

b e c: Catetos

Os catetos, representados por 'b' e 'c', são os lados que compõem o ângulo reto em um triângulo retângulo. Esses elementos desempenham um papel crucial na aplicação prática do Teorema de Pitágoras.

A relação matemática estabelecida por esse teorema depende do conhecimento preciso das medidas dos catetos para calcular a dimensão desconhecida. Sendo assim, entender as propriedades e as medidas desses lados é essencial para utilizar eficientemente o teorema e resolver problemas geométricos associados a triângulos retângulos.

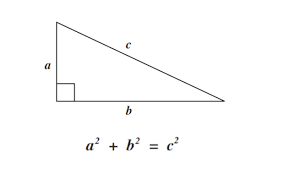
Aplicações Práticas do Teorema

O Teorema de Pitágoras, longe de ser uma teoria abstrata, desempenha um papel fundamental em diversas situações práticas do dia a dia e na resolução de problemas matemáticos. Imagine, por exemplo, a necessidade de medir a distância entre dois pontos em um terreno ou calcular o comprimento de um cabo que precisa ser estendido de um ponto a outro. Em ambas as situações, o teorema se revela como uma ferramenta essencial.

Essa aplicabilidade do Teorema de Pitágoras transcende o ambiente físico, encontrando espaço em questões matemáticas mais complexas. Em ambientes de avaliação, como o ENEM, a habilidade de aplicar esse teorema torna-se uma competência valiosa. Os problemas que envolvem raciocínio lógico e habilidades matemáticas frequentemente demandam a compreensão e aplicação eficaz desse teorema.

Dessa forma, ao entender as aplicações práticas do Teorema de Pitágoras, os estudantes não apenas aprimoram suas habilidades matemáticas, mas também desenvolvem uma visão mais ampla da utilidade da matemática no mundo real. Isso destaca a importância não apenas do conhecimento teórico, mas também da capacidade de transferir esse conhecimento para resolver problemas concretos e tomar decisões fundamentadas em diversas situações.

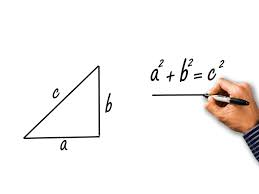
Como surgiu o Teorema de Pitágoras

O Teorema de Pitágoras é atribuído ao matemático grego Pitágoras, que viveu no século VI a.C. Pitágoras foi o fundador da Escola Pitagórica, uma comunidade de estudiosos que contribuíram significativamente para o desenvolvimento da matemática na antiguidade.

A história da criação do Teorema de Pitágoras é, em grande parte, envolta em lendas e mitos, e muitos detalhes específicos não são conhecidos com certeza. A narrativa mais comum é que Pitágoras e seus discípulos estavam interessados em descobrir relações entre os lados dos triângulos retângulos.

Segundo a tradição, os pitagóricos perceberam que, ao traçar quadrados nos lados de um triângulo retângulo, o quadrado construído sobre a hipotenusa era igual à soma dos quadrados construídos sobre os catetos. Essa descoberta foi formalizada no que hoje conhecemos como o Teorema de Pitágoras.

A formulação matemática do teorema, a² = b² + c², onde 'a' representa a hipotenusa e 'b' e 'c' são os catetos, tornou-se uma ferramenta essencial na geometria e é aplicada em diversas áreas, desde problemas práticos até ramos avançados da matemática. Embora a história exata da criação do teorema permaneça parcialmente obscura, sua influência duradoura e importância na matemática são incontestáveis.

Teorema de Pitágoras do Dia-a-dia

O Teorema de Pitágoras, embora seja um conceito fundamental na geometria, tem diversas aplicações práticas no dia a dia. Aqui estão algumas situações comuns em que você pode usar o Teorema de Pitágoras:

1. Medição de Distâncias:
   • Em trabalhos de construção, você pode usar o teorema para medir distâncias entre dois pontos. Por exemplo, ao verificar a distância entre cantos de uma sala para garantir que os móveis se encaixem adequadamente.
2. Navegação:
   • Ao planejar rotas ou calcular distâncias em um mapa, o Teorema de Pitágoras pode ser útil. Se você conhece as coordenadas (ou distâncias em linhas retas), pode calcular a distância total percorrida.
3. Construção e Design:
   • Em design de interiores, arquitetura e paisagismo, o teorema é usado para garantir proporções corretas e medidas precisas. Isso é essencial para evitar erros na construção.
4. Engenharia:
   • Engenheiros frequentemente aplicam o Teorema de Pitágoras para realizar cálculos em estruturas, como pontes, edifícios e estradas. Pode ser usado para garantir a estabilidade e a segurança dessas estruturas.
5. Problemas de Altura:
   • Se você precisa determinar a altura de um objeto inacessível (como uma árvore), pode usar o teorema em conjunto com a medição de ângulos para estimar a altura.
6. Tecnologia e Eletrônicos:
   • Em áreas como design de circuitos ou instalação de antenas, os princípios do Teorema de Pitágoras são aplicados para garantir que componentes estejam posicionados corretamente.
7. Ciências Naturais:
   • Em estudos geográficos, ambientais ou astronômicos, o teorema pode ser usado para calcular distâncias ou alturas inacessíveis.

Lembre-se de que o Teorema de Pitágoras é uma ferramenta versátil que pode ser aplicada em diversas situações cotidianas, tornando-se uma habilidade valiosa em várias áreas profissionais.