Prisma: Desvendando seus Segredos
Prisma: Desvendando seus Segredos
O prisma, uma figura geométrica de fascínio incontestável, assume uma função crucial nos estudos de geometria espacial, revelando-se como um sólido poliédrico convexo que cativa tanto estudantes quanto matemáticos. Este conteúdo não se limita a explorar os elementos fundamentais do prisma, mas também lança luz sobre suas classificações, características de bases e fórmulas intrínsecas. É fundamental salientar que a compreensão profunda desses conceitos não apenas enriquece o conhecimento matemático, mas também se configura como um conhecimento essencial em avaliações de grande relevância, como o ENEM.
O prisma, em sua essência, é um sólido poliédrico convexo que se destaca por suas características únicas. Ao desdobrar suas camadas, revelam-se elementos fundamentais como base, altura, arestas, vértices e faces laterais. Essa compreensão minuciosa não apenas aprimora a visualização tridimensional, mas também se revela vital para a resolução de problemas geométricos mais complexos.
Índice

Composição do Prisma
O prisma, objeto de estudo na geometria espacial, apresenta uma composição rica em elementos fundamentais, cada qual desempenhando um papel essencial na sua caracterização. Destacamos a seguir os componentes que constituem a essência do prisma:
Base
A base do prisma é um polígono que estabelece a fundação do sólido geométrico. A forma dessa base pode variar, influenciando diretamente as propriedades do prisma.
Altura
A altura do prisma é a distância vertical entre os planos das bases, proporcionando a dimensão vertical do sólido. Essa medida é crucial para cálculos relacionados ao volume e à área.
Arestas
As arestas são as linhas de interseção entre as faces do prisma. Elas conectam os vértices e delimitam as fronteiras do sólido, contribuindo para a sua definição tridimensional.
Vértices
Os vértices representam os pontos de encontro das arestas, constituindo os extremos do prisma. A análise dos vértices é essencial para compreender a configuração geométrica do sólido.
Faces Laterais
As faces laterais são planos que conectam as arestas correspondentes das bases, formando a "casca" do prisma. A quantidade e formato dessas faces variam de acordo com a geometria específica do sólido.
A compreensão detalhada desses elementos é fundamental para explorar as propriedades intrínsecas do prisma e calcular suas diversas características, enriquecendo assim o estudo da geometria espacial.
Classificação dos Prismas
Os prismas assumem uma posição proeminente na geometria espacial, sendo divididos em duas categorias principais: Reto e Oblíquo. Esta classificação, além de ampliar a compreensão da geometria espacial, destaca-se como um ponto crucial em questões de exames, como o ENEM.
Prisma Reto
O prisma reto é distintamente reconhecido por suas características específicas, sendo delineado por arestas laterais que são perpendicularmente alinhadas à base. Essa singularidade resulta em faces laterais que assumem a forma de retângulos. Compreender essas propriedades é não apenas essencial para distinguir o prisma reto, mas também se revela um conceito passível de ser testado em avaliações de matemática, incluindo o ENEM.
Prisma Oblíquo
Por outro lado, o prisma oblíquo apresenta uma configuração diferente, exibindo arestas laterais que são oblíquas em relação à base. Esse arranjo resulta em faces laterais em forma de paralelogramos, conferindo ao prisma uma estética distintiva. Identificar e compreender essas diferenças é crucial para a resolução de problemas envolvendo prismas em diversas situações, tornando-se um conhecimento valioso não apenas na geometria espacial, mas também em avaliações desafiadoras, como o ENEM.
O entendimento profundo das características de prismas retos e oblíquos não só enriquece o repertório de conhecimentos em geometria, mas também se destaca como um diferencial em questões que demandam aplicação prática desse saber, como em avaliações acadêmicas de alto nível.
Bases do Prisma
Bases do Prisma
As bases do prisma ocupam um papel de destaque em sua estrutura, desempenhando um papel significativo na sua classificação e identificação. A forma dessas bases é um fator determinante na categorização do prisma, conforme exploraremos detalhadamente a seguir.
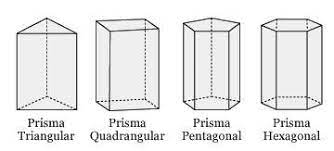
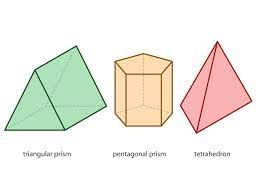
Prisma Triangular
Quando a base do prisma assume a forma de um triângulo, estamos diante de um prisma triangular. A compreensão das propriedades específicas deste tipo de prisma é fundamental para aplicar corretamente as fórmulas associadas, algo que pode ser explorado em questões de geometria em avaliações, incluindo o ENEM.
Prisma Quadrangular
Se a base do prisma é um quadrado, classificamo-lo como um prisma quadrangular. Essa característica não apenas influencia suas propriedades, mas também facilita a identificação e resolução de problemas matemáticos, inclusive em exames como o ENEM.
Prisma Pentagonal
Quando a base é um pentágono, o prisma recebe a designação de prisma pentagonal. Compreender suas características distintas é fundamental para explorar suas propriedades e resolver questões envolvendo esse tipo específico de prisma, que pode ser abordado em provas como o ENEM.
Prisma Hexagonal
A base do prisma hexagonal é um hexágono. Essa peculiaridade não apenas define sua classificação, mas também influencia diretamente o cálculo de diversas características geométricas. Esse conhecimento pode ser testado em exames, incluindo o ENEM.
Prisma Heptagonal
Um prisma com base em um heptágono é denominado prisma heptagonal. Essa característica específica não apenas o distingue de outros prismas, mas também é crucial para aplicar corretamente as fórmulas associadas. Tal entendimento é útil em questões de geometria presentes em avaliações, como o ENEM.
Prisma Octogonal
O prisma octogonal, com sua base em formato de octógono, apresenta propriedades únicas que o diferenciam de outros prismas. Compreender essas características é essencial para resolver problemas geométricos, uma habilidade que pode ser testada em exames, incluindo o ENEM.
A análise profunda das bases do prisma não apenas aprimora o entendimento da sua estrutura, mas também se revela como um conhecimento valioso em contextos acadêmicos e em avaliações que exigem uma aplicação prática desses conceitos, como o ENEM.
Fórmulas do Prisma
Cálculo da Área da Base
Determinar a área da base de um prisma é um passo crucial para a realização de cálculos subsequentes. A forma da base não é apenas um elemento estético; ela influencia diretamente o método de cálculo, tornando essencial compreender essas nuances para obter resultados precisos.
A Importância da Base na Geometria Prismática
A forma da base de um prisma varia, podendo ser um triângulo, quadrado, pentágono, hexágono, heptágono ou octógono, conforme suas categorizações. Cada formato demanda uma abordagem única no cálculo da área, destacando a importância de entender a relação direta entre a base e o método de cálculo.
Estratégias para Cálculo Preciso
Para prismas com base em formas regulares, como triângulos, quadrados ou hexágonos, a aplicação de fórmulas específicas é essencial. No caso de um prisma triangular, por exemplo, a área da base seria calculada considerando as dimensões do triângulo. Este mesmo princípio se aplica a outras formas.
Contextualização no ENEM
O entendimento profundo dessas estratégias não apenas enriquece a resolução de problemas matemáticos, mas também é uma habilidade valiosa em contextos avaliativos, como o ENEM. Questões envolvendo prismas frequentemente demandam a aplicação desses conceitos, ressaltando a importância de dominar o cálculo preciso da área da base.
Além do Básico: Desdobrando Desafios Geométricos
Compreender as nuances do cálculo da área da base não se limita a uma aplicação mecânica de fórmulas; é uma habilidade que permite abordar desafios geométricos mais complexos. Resolver questões que exigem a aplicação desses conhecimentos não só aprimora as habilidades matemáticas, mas também é um diferencial em avaliações, como o ENEM, que valorizam a capacidade de aplicar conhecimentos em situações práticas.
Em resumo, a habilidade de calcular a área da base de um prisma não é apenas um passo intermediário em problemas geométricos; é uma competência valiosa que se destaca em avaliações acadêmicas e na resolução de desafios matemáticos mais elaborados.
Áreas do Prisma
Calcular a área lateral e total do prisma é uma tarefa que envolve a aplicação de fórmulas específicas, as quais variam de acordo com a sua classificação e a forma da base. Essa análise aprofundada não só enriquece o entendimento das propriedades geométricas do prisma, mas também se destaca como uma habilidade chave em avaliações como o ENEM.
Variações nas Fórmulas de Área
A escolha da fórmula adequada para calcular a área lateral e total do prisma depende diretamente da sua classificação. Prismas podem ser retos ou oblíquos, e cada tipo requer abordagens específicas para determinar suas áreas. Além disso, a forma da base também desempenha um papel crucial, pois prismas podem ter bases triangulares, quadrangulares ou de outras formas, influenciando diretamente o método de cálculo.
Prisma Reto: Fórmulas Claras e Diretas
No caso de um prisma reto, cujas arestas laterais são perpendiculares à base, a fórmula para a área lateral é simplificada: a multiplicação do número de lados pela medida da face lateral. A área total, por sua vez, inclui a soma das áreas laterais e das áreas das bases. Dominar essas fórmulas é crucial para resolver problemas geométricos em avaliações, como o ENEM.
Prisma Oblíquo: Adaptando-se às Inclinações
Já no prisma oblíquo, onde as arestas laterais são oblíquas em relação à base, as fórmulas para área lateral e total se ajustam para acomodar essa inclinação. A precisão na aplicação dessas fórmulas é vital para obter resultados corretos em questões que exigem o cálculo das áreas em contextos práticos.
Volume do Prisma
O volume do prisma, uma grandiosidade geométrica essencial em diversas aplicações, revela-se como um cálculo fundamental. Esse processo, que leva em consideração a área da base e a altura, não apenas enriquece a compreensão das propriedades geométricas do prisma, mas também se destaca como uma habilidade crucial em avaliações, como o ENEM.
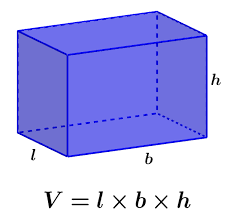
Integrando Área da Base e Altura
O cálculo do volume do prisma é um exemplo clássico de como a área da base e a altura estão intrinsecamente conectadas. A fórmula fundamental, que multiplica a área da base pela altura, reflete a quantidade de espaço contido dentro do sólido geométrico. A aplicação dessa fórmula é essencial para determinar volumes precisos em diversas situações práticas.
Prismas Regulares e suas Singularidades
Em casos específicos, quando as bases do prisma são polígonos regulares, como quadrados ou triângulos, o cálculo do volume se torna ainda mais direto. Esses chamados "prismas regulares" possuem fórmulas específicas que simplificam o processo de determinação do volume. Por exemplo, se todas as faces do prisma forem quadradas, estamos diante de um cubo; se todas as faces forem paralelogramos, temos um paralelepípedo.
Conexões com o ENEM: Aplicações em Contexto
O entendimento profundo do cálculo do volume do prisma não só é valioso em contextos práticos, mas também se destaca em avaliações como o ENEM. Questões que envolvem a determinação de volumes, muitas vezes, exigem a aplicação desses conceitos em contextos do cotidiano, realçando a relevância dessa habilidade no cenário acadêmico e além.
Além do Cálculo: Aplicações no Mundo Real
Entender o volume do prisma transcende a aplicação de fórmulas matemáticas; é uma habilidade que se traduz em aplicações práticas no mundo real. Seja no design de embalagens, na arquitetura ou em outras disciplinas, a capacidade de calcular o volume de prismas é uma competência valiosa.
Em resumo, desvendar o volume do prisma não é apenas uma exploração matemática; é uma jornada que conduz a uma compreensão mais profunda das propriedades geométricas e destaca-se como uma habilidade essencial tanto em avaliações quanto em aplicações do mundo real.

