Números Racionais: Explorando Suas Características e Subconjuntos

Os números racionais desempenham um papel crucial no domínio da matemática, abrangendo valores que se prestam a serem expressos na forma de frações e que podem igualmente ser representados por decimais finitos ou periódicos. Este conjunto ocupa uma posição hierárquica que engloba tanto os números naturais quanto os inteiros.

Os números racionais podem ser conceituados como valores expressos na forma de fração (a/b), onde a e b são inteiros e b não é zero. Esta definição é fundamentada na inter-relação entre os conjuntos numéricos, indicando que todo número natural é, por extensão, um número inteiro, e todo número inteiro, por sua vez, é um número racional.

Definição e Representação dos Números Racionais

A compreensão do conjunto dos números racionais envolve sua representação matemática fundamental, estabelecendo que qualquer número racional, expresso como a/b (onde a e b são inteiros, e b não é zero), pertence ao conjunto dos números inteiros. Essa definição destaca uma relação intrínseca, evidenciando que todo número natural também é categorizado como número inteiro, e, por sua vez, todo número inteiro é classificado como número racional. Essa interconexão reforça a base conceitual dos números racionais e sua inserção em um contexto mais amplo dentro da hierarquia numérica.

Exemplos de Números Racionais

Números Inteiros

Os números inteiros constituem uma categoria específica dentro do conjunto dos números racionais, e sua representação evidencia uma relação intrínseca entre essas duas classes numéricas. Ao considerarmos exemplos, fica claro que os números inteiros podem ser expressos como uma divisão de dois números inteiros. Por exemplo, 2/1 é equivalente a 5/1, que, por sua vez, é igual a -7/1. Essa equiparação destaca não apenas a diversidade numérica presente nos inteiros, mas também reforça a inclusão desses valores no conjunto mais amplo dos números racionais. Essa interconexão enriquece nossa compreensão sobre a estrutura e as relações entre diferentes tipos de números.

Números Decimais Finitos

Os números decimais finitos constituem uma categoria específica no conjunto dos números racionais. Sua representação matemática revela uma conexão intrínseca com os números inteiros. Quando analisamos exemplos específicos, como 0,2 e 0,06, podemos observar que esses números decimais finitos podem ser expressos como uma divisão entre dois números inteiros. Por exemplo, 0,2 é equivalente a 2/10, e 0,06 é igual a 6/100. 

Essa equivalência destaca a capacidade de representar números decimais finitos em termos de frações, evidenciando a riqueza de relações entre diferentes tipos de números racionais. Essa compreensão aprofundada não apenas fortalece nosso conhecimento matemático, mas também destaca a interconexão entre as diversas representações dos números racionais.

Números Periódicos (Dízimas Periódicas)

Os números periódicos, também conhecidos como dízimas periódicas, representam uma categoria intrigante dentro do conjunto dos números racionais. Estes são números decimais com uma quantidade infinita de casas decimais que se repetem de maneira regular. Ao explorarmos exemplos específicos, como 0,333... e 0,24141..., torna-se evidente que esses números periódicos podem ser expressos de forma precisa como frações. Por exemplo, 0,333... é equivalente a 1/3, e 0,24141... pode ser representado como 239/990. 

Essa equivalência demonstra a fascinante capacidade de traduzir números periódicos complexos em formas mais simplificadas por meio de frações. Compreender essa relação entre a representação decimal periódica e as frações não apenas enriquece nosso conhecimento matemático, mas também destaca a harmonia subjacente entre diferentes expressões dos números racionais.

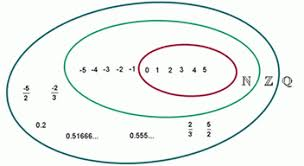
Subconjuntos dos Números Racionais

Racionais Não-Nulos

Dentro do vasto universo dos números racionais, destacamos um subconjunto intrigante: os Racionais Não-Nulos. Este grupo específico é composto por todos os números racionais, com a única ressalva de excluir o zero. Vamos aprofundar nossa compreensão dessa categoria especial:

Definição e Representação Matemática

Matematicamente, os Racionais Não-Nulos são representados como x ∈ ℚ | x ≠ 0. Essa expressão sublinha que qualquer número racional presente nesse conjunto é diferente de zero. Essa condição estabelece uma distinção clara em relação aos demais subconjuntos de racionais.

Características Distintivas

Ao explorarmos esse conjunto, percebemos que abrange tanto os números racionais positivos quanto os números racionais negativos, unindo-os sob a condição compartilhada de não serem nulos. Essa peculiaridade ressalta a diversidade presente nesse subconjunto, oferecendo uma visão abrangente da variedade dos números racionais.

Relevância e Aplicações

A compreensão dos Racionais Não-Nulos é crucial em diversas áreas da matemática, desde equações algébricas até a análise de proporções em situações do mundo real. A exclusão do zero confere a esse subconjunto propriedades únicas, tornando-o fundamental em contextos que demandam considerações específicas.

Ao examinarmos os Racionais Não-Nulos, não apenas fortalecemos nossa compreensão dos números racionais, mas também reconhecemos a importância de suas propriedades em aplicações práticas. Esse enfoque detalhado é valioso tanto para estudantes que exploram conceitos fundamentais quanto para aqueles que buscam uma compreensão mais aprofundada dos números racionais em contextos mais avançados.

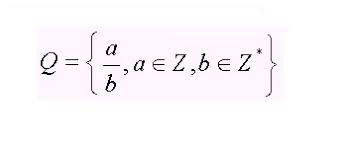
Racionais Não-Negativos

Analisando os Racionais Não-Negativos: Uma Perspectiva Abrangente

Dentro do contexto dos números racionais, destacamos um subconjunto fundamental e versátil: os Racionais Não-Negativos. Esse grupo abarca tanto os números racionais positivos quanto o zero, oferecendo uma variedade de propriedades matemáticas dignas de exploração:

Definição e Expressão Matemática

Os Racionais Não-Negativos são representados de maneira concisa na linguagem matemática como x ∈ ℚ+ | x ≥ 0. Essa formulação enfatiza que qualquer número racional presente nesse conjunto é maior ou igual a zero, incluindo o próprio zero. Essa inclusão do zero traz nuances interessantes às propriedades desse subconjunto.

Características e Comportamento

Ao examinarmos esse conjunto, percebemos que ele abrange uma gama diversificada de valores, desde o zero até números racionais positivos. Essa característica confere aos Racionais Não-Negativos uma importância particular em situações onde a ausência de valores negativos é relevante. Em muitos contextos matemáticos e aplicativos práticos, esse subconjunto desempenha um papel crucial.

Aplicações Práticas e Significado

A compreensão dos Racionais Não-Negativos é essencial em várias disciplinas, desde a resolução de equações até a modelagem de fenômenos do mundo real. A inclusão do zero neste conjunto destaca a presença de situações onde a ausência de uma quantidade é tão significativa quanto a presença de valores positivos. Isso enriquece a aplicabilidade desse subconjunto em cenários diversos.

Explorar os Racionais Não-Negativos não apenas amplia nosso entendimento dos números racionais, mas também destaca a importância desses valores em diferentes contextos. Esse enfoque minucioso não apenas beneficia estudantes que estão consolidando conceitos fundamentais, mas também serve como base sólida para aqueles que se aprofundam em aplicações mais avançadas.

Racionais Não-Positivos

Desvendando os Racionais Não-Positivos: Uma Análise Profunda

Dentro do vasto campo dos números racionais, destaca-se um subconjunto intrigante e versátil: os Racionais Não-Positivos. Este grupo abarca tanto os números racionais negativos quanto o zero, oferecendo uma gama diversificada de propriedades matemáticas e aplicações práticas:

Definição e Formulação Matemática

Os Racionais Não-Positivos são formalmente expressos na linguagem matemática como x ∈ ℚ- | x ≤ 0. Essa notação destaca que qualquer número racional pertencente a esse conjunto é menor ou igual a zero, incluindo o próprio zero. Essa inclusão do zero é significativa, trazendo implicações únicas ao comportamento e às características desse subconjunto.

Propriedades e Comportamento

Ao examinarmos esse conjunto, observamos que ele abrange desde o zero até números racionais negativos. Essa amplitude confere aos Racionais Não-Positivos uma relevância notável em situações onde a presença de valores negativos ou a ausência de valores positivos é crítica. Essa dualidade torna esse subconjunto uma ferramenta matemática flexível em diversos contextos.

Aplicações e Importância Prática

A compreensão dos Racionais Não-Positivos é vital em várias disciplinas, desde a modelagem de fenômenos financeiros até a análise de dados que envolvem débitos ou reduções. A inclusão dos números racionais negativos e do zero destaca-se em cenários onde a ausência de valores positivos é tão crucial quanto a presença de valores negativos. Essa característica torna esse subconjunto valioso em contextos práticos e teóricos.

Explorar os Racionais Não-Positivos não apenas enriquece nosso entendimento dos números racionais, mas também ressalta a relevância desses valores em situações onde a negatividade é uma consideração fundamental. Este enfoque detalhado não apenas beneficia estudantes que estão consolidando conceitos fundamentais, mas também oferece uma base sólida para aqueles que desejam explorar aplicações mais avançadas.

Racionais Positivos e Negativos

Desbravando os Racionais Positivos e Negativos: Uma Exploração Detalhada

Dentro do vasto universo dos números racionais, emergem dois subconjuntos distintos e essenciais: os Racionais Positivos e os Racionais Negativos. Esses conjuntos, quando explorados em conjunto, revelam propriedades e aplicações matemáticas valiosas:

Racionais Positivos: Além do Zero

Os Racionais Positivos, denotados como (x ∈ ℚ+) e menores que zero (x ∈ ℚ-) formam um conjunto abrangente que inclui todos os números racionais maiores que zero. Esses números desempenham um papel fundamental em diversas áreas, desde cálculos financeiros até análises estatísticas. A exclusão do zero destaca a positividade desses valores, tornando-os cruciais em contextos onde apenas ganhos ou valores positivos são relevantes.

Racionais Negativos: Explorando o Lado Menos Convencional

Os Racionais Negativos, representados como �∈�− ∣ �<0x∈Q− ∣ x<0, formam o conjunto daqueles números racionais menores que zero. Esses números desempenham um papel crucial na modelagem de dívidas, débitos e situações onde as quantidades estão abaixo da referência zero. A inclusão dos Racionais Negativos complementa o conjunto dos positivos, proporcionando uma visão abrangente dos números racionais.

Interseção e Complementaridade

Ao analisarmos conjuntamente os Racionais Positivos e Negativos, percebemos que juntos abrangem toda a reta numérica, excluindo o zero. Essa característica destaca a complementaridade desses conjuntos e sua capacidade de cobrir toda a gama de valores racionais, desde ganhos até perdas.

Relevância Prática e Aplicações

A compreensão profunda dos Racionais Positivos e Negativos é crucial em diversos contextos, incluindo finanças, estatísticas e modelagem matemática. Esses conjuntos desempenham um papel essencial na interpretação de dados, cálculos de taxas de crescimento e na representação de valores que variam em ambas as direções da reta numérica.

Explorar os Racionais Positivos e Negativos oferece uma visão abrangente da diversidade dos números racionais e suas aplicações em cenários do mundo real. Esta análise não apenas fortalece a compreensão fundamental desses conceitos, mas também fornece uma base sólida para abordagens mais avançadas em matemática e disciplinas relacionadas.

Relevância para o ENEM

O entendimento abrangente sobre os números racionais e seus subconjuntos é fundamental para resolver questões complexas de matemática, sendo um tema recorrente em avaliações como o Exame Nacional do Ensino Médio (ENEM). Dominar esses conceitos não apenas fortalece as habilidades matemáticas, mas também contribui para uma base sólida em diversos campos da ciência e engenharia.