Explorando os Números Reais: Uma Jornada pelos Conjuntos Numéricos

O mundo dos números reais é um verdadeiro oceano, onde mergulhamos nas profundezas dos conjuntos que vão além dos simples números naturais. Esta exploração nos conduz desde os contáveis números inteiros até os enigmáticos números irracionais.

Este artigo visa desvendar essa intrincada rede de conjuntos, proporcionando uma compreensão abrangente e multifacetada. É importante ressaltar que essa compreensão não apenas enriquece o conhecimento matemático, mas também se revela valiosa em avaliações como o ENEM, que valoriza a interdisciplinaridade e a capacidade de relacionar conceitos.

Portanto, ao embarcar nessa jornada pelos números reais, estamos não apenas explorando o intricado mundo da matemática, mas também adquirindo ferramentas essenciais para enfrentar desafios acadêmicos e, especificamente, para enfrentar questões que possam surgir em avaliações como o ENEM.

1. Conceito e Representação dos Números Reais

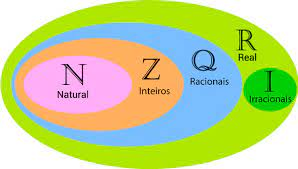
Os números reais, denotados por R, constituem uma rica tapeçaria matemática que abraça quatro conjuntos fundamentais: naturais (N), inteiros (Z), racionais (Q), e irracionais (I). Cada conjunto, em sua essência, carrega propriedades únicas e desempenha um papel vital no mosaico dos números reais.

A representação formal dos números reais como a união dos conjuntos N, Z, Q, e I, expressa-se pela equação R = N U Z U Q U I. Essa composição, de modo mais conciso, pode ser expressa como R = Q U I, destacando a importância dos conjuntos racionais e irracionais nesse vasto domínio numérico.

Explorar o conjunto dos números reais é embarcar em uma jornada pelo tecido intricado da matemática, onde cada conjunto adiciona uma nuance única. O entendimento desses conjuntos não apenas enriquece a compreensão matemática, mas também fornece uma base sólida para abordar questões complexas que podem surgir em avaliações como o ENEM, onde a aplicação interdisciplinar do conhecimento é essencial.

2. Diagrama dos Conjuntos Numéricos: Uma Visualização Esclarecedora

O diagrama dos conjuntos numéricos é uma ferramenta poderosa que desvenda as complexas interconexões entre os conjuntos matemáticos. Ao mergulharmos nessa visualização, somos guiados por uma jornada esclarecedora pela vastidão dos números, compreendendo como cada conjunto se entrelaça harmoniosamente.

Neste panorama, o conjunto dos números reais (R) se destaca como o epicentro, envolvendo quatro conjuntos principais: naturais (N), inteiros (Z), racionais (Q), e irracionais (I). O diagrama numérico não apenas revela a inclusão de conjuntos menores no conjunto dos números reais, mas também ilustra vividamente a diversidade e riqueza matemática que cada conjunto agrega.

Essa ferramenta visual não só aprimora a compreensão dos relacionamentos intrínsecos entre os conjuntos, mas também serve como um recurso valioso para quem se prepara para avaliações como o ENEM, onde a interpretação gráfica e a habilidade de relacionar conceitos são fundamentais para o sucesso.

3. Relações entre os Conjuntos: Números Inteiros, Naturais e Racionais

Ao adentrarmos nas relações intricadas entre os conjuntos numéricos, deparamo-nos com uma teia matemática fascinante. A análise minuciosa revela que o conjunto dos números racionais (Q) é, na verdade, uma aliança harmoniosa dos conjuntos naturais (N) e inteiros (Z).

Essa interligação sugere que cada número inteiro (Z) é, por sua própria natureza, um número racional (Q), destacando a inclusão de Z em Q. A complexidade das relações não termina aí, pois o conjunto dos números inteiros (Z) abraça os números naturais (N), demonstrando que todo número natural (N) é, por definição, um número inteiro (Z).

Desvendar essas relações não apenas enriquece nossa compreensão da matemática, mas também se revela como um conhecimento valioso em avaliações como o ENEM, onde a habilidade de discernir interconexões entre conceitos é uma competência essencial.