Explorando as Profundezas da Trigonometria no Triângulo Retângulo

O estudo da trigonometria no triângulo retângulo proporciona uma compreensão rica sobre triângulos que contêm um ângulo interno de 90°, conhecido como ângulo reto. A trigonometria, ciência que explora as relações entre os triângulos, mergulha nas complexidades das figuras geométricas planas, com seus três lados e três ângulos internos.

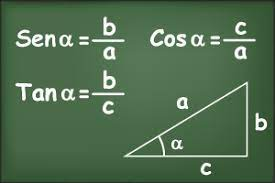
Complexidade e Variedade dos Triângulos:

Antes de mergulharmos nas intricadas relações trigonométricas, é imperativo compreender a riqueza e diversidade que os triângulos apresentam. Eles não são simplesmente figuras geométricas, mas manifestações de formas únicas e propriedades distintas.

Variedade de Configurações:

1. Triângulo Equilátero:
   • Todos os lados são iguais, proporcionando uma simetria perfeita. É a expressão máxima da igualdade nas formas triangulares.
2. Triângulo Isósceles:
   • Possui dois lados iguais, enquanto o terceiro lado difere em comprimento. Esta configuração cria uma simetria que ressalta a igualdade de dois dos seus lados.
3. Triângulo Escaleno:
   • Todos os lados possuem medidas distintas. É a expressão da diversidade e individualidade no mundo dos triângulos, onde nenhum lado é igual ao outro.

Classificação dos Ângulos Internos:

Os ângulos internos dos triângulos desempenham um papel crucial na sua classificação e compreensão.

1. Ângulos Obtusângulos:
   • São ângulos internos que excedem 90°. Eles proporcionam uma dinâmica peculiar aos triângulos, conferindo-lhes uma natureza mais ampla e aberta.
2. Ângulos Acutângulos:
   • Ângulos internos que são menores que 90°, conferindo uma sensação de compacticidade e foco aos triângulos. Essa categoria destaca a agudeza característica desses ângulos.

Soma dos Ângulos Internos:

Independentemente da configuração específica, todos os triângulos compartilham uma propriedade fundamental: a soma total dos seus ângulos internos é sempre 180°. Essa constante matemática cria uma harmonia intrínseca entre os ângulos, independentemente das suas formas ou medidas individuais.

Ao compreender a diversidade de configurações e as características intrínsecas dos triângulos, estabelecemos uma base sólida para adentrar o fascinante mundo das relações trigonométricas. Essa compreensão prévia não apenas enriquece nossa abordagem, mas também destaca a beleza e complexidade inerentes às formas geométricas.

Explorando Detalhadamente os Componentes e Relações do Triângulo Retângulo:

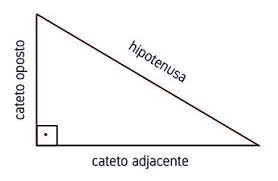
Composição do Triângulo Retângulo:

O triângulo retângulo, uma figura geométrica intrigante, possui elementos distintos que desempenham papéis fundamentais na sua estrutura.

1. Catetos:
   • São os lados que formam o ângulo reto, proporcionando uma base sólida para a formação do triângulo. A interação entre esses catetos é essencial para a dinâmica interna do triângulo.
2. Hipotenusa:
   • O lado oposto ao ângulo reto é conhecido como hipotenusa. Além de ser a face mais extensa do triângulo, ela desempenha um papel crucial nas relações métricas e na determinação das razões trigonométricas.

Teorema de Pitágoras:

O Teorema de Pitágoras, uma conquista notável da matemática, estabelece uma relação fundamental no contexto dos triângulos retângulos:

ℎ2=��2+��2h2=ca2+co2

Essa equação afirma que o quadrado da hipotenusa (ℎh) é igual à soma dos quadrados dos catetos (��ca e ��co). Essa fórmula, simples em sua expressão, revela uma profunda conexão entre os lados do triângulo, proporcionando uma base sólida para explorar suas propriedades.

Razões Trigonométricas:

As relações trigonométricas no triângulo retângulo oferecem uma perspectiva única sobre a interação entre seus elementos. Estas são expressas através de três fundamentais razões trigonométricas:

1. Seno (sin⁡sin):
   • Representa a razão entre o cateto oposto e a hipotenusa (sin⁡�=��ℎsinθ=hco​). Esta razão destaca a verticalidade em relação à hipotenusa.
2. Cosseno (cos⁡cos):
   • É a razão entre o cateto adjacente e a hipotenusa (cos⁡�=��ℎcosθ=hca​). Enfatiza a horizontalidade em relação à hipotenusa.
3. Tangente (tan⁡tan):
   • Definida como a razão entre o cateto oposto e o cateto adjacente (tan⁡�=����tanθ=caco​). Representa a inclinação do triângulo em relação à base.

Ao compreender minuciosamente esses elementos e relações no contexto do triângulo retângulo, a matemática revela-se não apenas como uma ferramenta de cálculos, mas como um meio fascinante de explorar e compreender as complexidades geométricas que cercam essa figura tão especial.

Explorando o Círculo Trigonométrico e suas Complexidades:

Círculo Trigonométrico como Ferramenta Crucial:

O círculo trigonométrico, um recurso essencial na matemática, não é apenas uma representação visual, mas uma poderosa ferramenta para compreender as relações trigonométricas. Seu eixo vertical destina-se ao seno, enquanto o horizontal ao cosseno. Esta disposição cria uma estrutura que transcende a simples visualização, proporcionando uma compreensão profunda das relações angulares.

1. Eixo Vertical (Seno):
   • Representa a altura em relação à circunferência, destacando a verticalidade e a amplitude dos ângulos.
2. Eixo Horizontal (Cosseno):
   • Reflete a horizontalidade e a extensão angular, revelando as relações entre os ângulos e a base do círculo.

Razões Inversas e a Amplitude do Círculo:

Além das razões trigonométricas tradicionais, o círculo trigonométrico também explora as razões inversas: secante, cossecante e cotangente. Estas, ao contrário das razões tradicionais, proporcionam uma visão inversa, enfocando a complementaridade das relações angulares.

1. Secante (sec⁡sec):
   • Representa a razão entre a hipotenusa e o cateto adjacente (sec⁡�=ℎ��secθ=cah​). Destaca a influência da amplitude angular na relação entre os lados do triângulo.
2. Cossecante (csc⁡csc):
   • É a razão entre a hipotenusa e o cateto oposto (csc⁡�=ℎ��cscθ=coh​). Enfatiza a complementaridade vertical em relação à hipotenusa.
3. Cotangente (cot⁡cot):
   • Definida como a razão entre o cateto adjacente e o cateto oposto (cot⁡�=����cotθ=coca​). Representa a inclinação inversa do triângulo em relação à base.

Ângulos Notáveis e Suas Implicações:

Os ângulos notáveis, frequentemente encontrados em problemas trigonométricos, desempenham um papel crucial. Para 30°, 45° e 60°, as relações trigonométricas específicas proporcionam uma base sólida para a resolução de problemas mais complexos. Esses ângulos, ao serem identificados como notáveis, simplificam a abordagem de situações desafiadoras, oferecendo atalhos valiosos na análise trigonométrica.

Ao compreender plenamente o círculo trigonométrico e suas ramificações, a matemática revela-se não apenas como uma disciplina de cálculos, mas como uma linguagem intricada para decifrar as complexidades das relações angulares e geométricas.

Exercício Resolvido:

Em um exemplo prático, a aplicação das relações trigonométricas é evidenciada. Dado um triângulo retângulo com hipotenusa de 8 cm e um ângulo interno de 30°, os catetos oposto (x) e adjacente (y) são determinados utilizando seno e o Teorema de Pitágoras.

Esse exercício resolvido destaca a aplicação direta da trigonometria no contexto prático, enfatizando a utilidade desses conceitos na resolução de problemas geométricos.

Ao explorarmos a trigonometria no triângulo retângulo, não apenas adentramos o mundo das relações geométricas, mas também percebemos sua aplicabilidade em situações do cotidiano, enriquecendo nossa compreensão da matemática e suas aplicações práticas.

O exercício proposto envolve um triângulo retângulo com hipotenusa de 8 cm e um ângulo interno de 30°. Vamos aplicar as relações trigonométricas para encontrar os catetos oposto (�x) e adjacente (�y).

Utilizando o Seno:

O seno do ângulo de 30° é dado por:

sin⁡30°=cateto oposto(�)hipotenusasin30°=hipotenusacateto oposto(x)​

12=�821​=8x​

�=4x=4

Portanto, o cateto oposto (�x) mede 4 cm.

Utilizando o Teorema de Pitágoras:

Segundo o Teorema de Pitágoras, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa:

h2=ca2+co2

82=�2+4282=y2+42

64=�2+1664=y2+16

�2=48y2=48

�=48y=48​

Portanto, o cateto adjacente (�y) mede 4848​ cm.

Conclusão:

Os lados do triângulo retângulo são encontrados como 88 cm (hipotenusa), 44 cm (cateto oposto) e 4848​ cm (cateto adjacente). Além disso, os ângulos internos são 30°30° (acutângulo), 90°90° (reto) e 60°60° (acutângulo), evidenciando que a soma dos ângulos internos dos triângulos sempre totaliza 180°180°.

Esse exemplo prático reforça a aplicação eficaz das relações trigonométricas na resolução de problemas geométricos, ressaltando a importância desses conceitos não apenas como abstrações matemáticas, mas como ferramentas valiosas para compreender e resolver situações do mundo real.