Desvendando a Área do Triângulo: Múltiplos Métodos e Fórmulas

Adentrar no intrigante universo da geometria plana nos conduz à figura mágica do triângulo, uma entidade com três lados repleta de segredos matemáticos. A tarefa crucial de compreender e calcular a área desse polígono é uma jornada fascinante, e é nesse guia que desvendaremos múltiplos métodos para realizar essa proeza.

Seja você um estudante se preparando para uma desafiadora prova escolar ou um aspirante ao ENEM, dominar os intricados caminhos da área do triângulo é um conhecimento que transcende os limites da sala de aula. Neste guia abrangente, mergulharemos em diferentes técnicas e fórmulas que possibilitam o cálculo preciso da área do triângulo, fornecendo não apenas respostas, mas também insights valiosos para o entendimento mais profundo da geometria. Prepare-se para desvendar os mistérios dessa figura poligonal e elevar suas habilidades matemáticas a novos patamares.

Índice:

1. Como calcular a área de um triângulo 
   1.1 Área do Triângulo Isósceles
   1.2 Área do Triângulo Retângulo
   1.3 Área do Triângulo Equilátero
   1.4 Área do Triângulo Escaleno
   
2. Outras Fórmulas para Calcular a Área do Triângulo
   2.1 Fórmula de Heron
   2.2 Fórmula do Raio Circunscrito

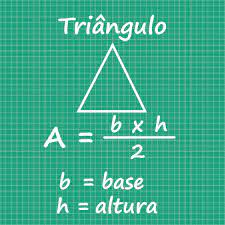
1. Como Calcular a Área de um Triângulo?

Na maioria das situações, a fórmula básica para calcular a área do triângulo é amplamente aplicável, utilizando as medidas da base e da altura: Área (A) = (Base * Altura) / 2. No entanto, cada tipo de triângulo apresenta nuances únicas que influenciam a escolha do método de cálculo.

1.1 Área do Triângulo Isósceles

O triângulo isósceles, caracterizado por dois lados e dois ângulos congruentes, traz consigo um desafio na hora de calcular sua área. A altura relativa à base desempenha um papel crucial nesse processo, e o Teorema de Pitágoras se revela uma ferramenta valiosa para essa tarefa.

Exemplo: Como calcular a área de um triângulo isósceles?

1.2 Área do Triângulo Retângulo

Com um ângulo reto (90º) e dois ângulos agudos, o triângulo retângulo traz simplicidade. Suas características permitem o uso do Teorema de Pitágoras para encontrar a altura e calcular a área.

Exemplo: Descubra a área de um triângulo retângulo conhecendo seus lados.

1.3 Área do Triângulo Equilátero

O triângulo equilátero, com lados e ângulos iguais, apresenta uma relação especial. O Teorema de Pitágoras auxilia na obtenção da altura, permitindo calcular a área de forma eficaz.

Exemplo: Calcule a área de um triângulo equilátero conhecendo apenas um lado.

1.4 Área do Triângulo Escaleno

Com lados e ângulos distintos, o triângulo escaleno demanda métodos avançados, incluindo trigonometria. O conhecimento de dois lados e o ângulo entre eles é essencial para aplicar a fórmula correta.

Exemplo: Calcule a área de um triângulo escaleno conhecendo dois lados e o ângulo entre eles.

2. Outras Fórmulas para Calcular a Área do Triângulo

2.1 Fórmula de Heron

A "Fórmula de Heron" surge como uma alternativa valiosa para calcular a área de um triângulo. Baseada nos semiperímetros e nos lados da figura, essa fórmula proporciona uma abordagem eficiente, eliminando a necessidade de conhecer a medida da altura. 

O "Teorema de Heron" simplifica o processo de cálculo da área, tornando-se uma ferramenta valiosa em situações em que a altura não está prontamente disponível. Essa versatilidade a torna uma opção estratégica ao explorar diferentes métodos para encontrar a área do triângulo.

2.2 Fórmula do Raio Circunscrito

A "Fórmula do Raio Circunscrito" ganha destaque quando lidamos com triângulos inscritos numa circunferência. Esta fórmula, que tem como base a "Lei dos Senos", revela sua utilidade ao considerar os lados do triângulo e o raio da circunferência circunscrita. Ao compreender e aplicar essa fórmula, torna-se possível calcular a área de forma eficiente em situações específicas.

Dominar esses métodos não apenas amplia a compreensão sobre a área do triângulo, mas também prepara o caminho para o sucesso em avaliações escolares. Além disso, a aplicação desses conhecimentos pode se estender a exames desafiadores, como o ENEM, proporcionando uma base sólida para enfrentar problemas geométricos mais complexos com confiança e precisão.

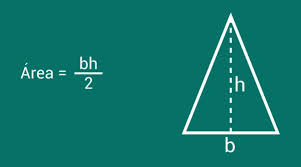
Como calcular a área de um triângulo?

O cálculo da área do triângulo é essencial e, na maioria das situações, é realizado multiplicando a base pela altura e dividindo o resultado por dois. Essa fórmula básica, Área = (Base * Altura) / 2, é amplamente aplicada, mas vale destacar que existem outras formas de calcular a área, dependendo das informações disponíveis sobre o triângulo.

Para encontrar a área do triângulo, basta seguir a fórmula mencionada, em que a base e a altura são cruciais para o resultado final. Essa compreensão básica é fundamental não apenas para o entendimento matemático, mas também para resolver problemas geométricos variados.

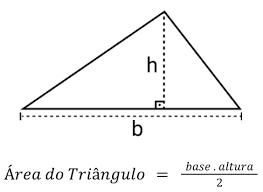
Como calcular a área de um triângulo retângulo?

O cálculo da área de um triângulo retângulo é uma tarefa simples e eficiente. Para realizar esse processo, basta multiplicar a base (representada por "b") pela altura (indicada por "h") e, em seguida, dividir o resultado por 2. 

Essa fórmula básica, Área = (b * h) / 2, proporciona uma abordagem direta para determinar a extensão da região ocupada por esse tipo específico de triângulo. Essa compreensão é crucial para estudantes que se preparam para avaliações como o ENEM, pois a área de triângulos retângulos frequentemente figura em questões matemáticas. 

Dominar esse cálculo não apenas fortalece as habilidades matemáticas, mas também contribui para o sucesso em diversas provas e exames.

Como calcular a área de um triângulo de três lados diferentes?

O triângulo escaleno, caracterizado por três lados distintos, desafia os estudantes a explorarem uma fórmula específica para calcular sua área. Diferentemente de triângulos com lados iguais, o escaleno exige uma abordagem mais complexa. Para determinar a área desse triângulo, multiplicamos as medidas da base e da altura e, crucialmente, dividimos esse produto por 2. A fórmula fundamental para a área de um triângulo escaleno é expressa como Área = (Base * Altura) / 2.

Compreender esse cálculo é vital para quem se prepara para avaliações escolares e exames, pois o tema frequentemente figura em questões matemáticas. Além de fornecer um conhecimento prático sobre a área desse tipo específico de triângulo, a compreensão dessa fórmula aprimora as habilidades matemáticas dos estudantes, contribuindo para o sucesso em suas jornadas acadêmicas.

Como calcular a área de um triângulo obtuso?

Quando se trata de triângulos obtusos, cujos ângulos são maiores que 90 graus, o cálculo da área exige uma abordagem cuidadosa. Diferentemente dos triângulos convencionais, os obtusos desafiam os estudantes a aplicar uma fórmula específica para determinar a área de forma precisa. Para realizar esse cálculo, multiplicamos o comprimento da base pela altura e, em seguida, dividimos esse produto por 2. A expressão matemática que descreve esse processo é fundamental para quem enfrenta questões envolvendo triângulos obtusos em avaliações escolares e exames.

Compreender essa fórmula não apenas fornece uma maneira eficiente de calcular a área de triângulos obtusos, mas também desenvolve as habilidades matemáticas dos estudantes. Esse conhecimento prático é valioso para a resolução de problemas geométricos mais complexos, consolidando a compreensão da matemática e preparando os alunos para o sucesso acadêmico.