A Importância da Área do Círculo na Geometria

A área do círculo é um conceito fundamental na geometria, sendo essencial para diversas aplicações em matemática e em outras áreas do conhecimento. Compreender como calcular a área de um círculo não apenas amplia o nosso entendimento sobre figuras geométricas planas, mas também nos permite resolver uma variedade de problemas práticos que envolvem medidas de superfície.

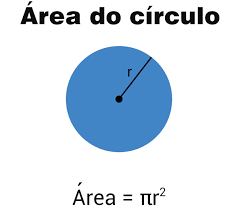
Fórmula da Área do Círculo

Para calcular a área de um círculo, utilizamos uma fórmula simples, mas poderosa:

�=�⋅�2A=π⋅r2

Onde:

• �π é a constante Pi, aproximadamente igual a 3,1415.
• �r é o raio do círculo.

É importante destacar que o raio representa a distância do centro do círculo até sua extremidade. Ou seja, qualquer linha que conecte o centro do círculo a um ponto em sua borda é considerada um raio.

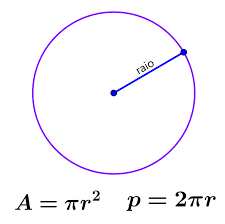
Compreendendo o Perímetro do Círculo

Além da área, outra medida importante relacionada ao círculo é o seu perímetro, que é comumente chamado de circunferência. O perímetro de uma figura geométrica é a soma de todos os seus lados, medindo o comprimento total do contorno da figura.

No caso do círculo, o perímetro é representado pela circunferência e pode ser calculado usando a seguinte fórmula:

�=2�⋅�P=2π⋅r

Essa fórmula nos diz que o perímetro da circunferência é igual a duas vezes o produto da constante Pi pelo raio do círculo. Em outras palavras, o perímetro é o comprimento da linha que forma a borda do círculo.

Aplicações Práticas

Entender a área e o perímetro do círculo é crucial em várias situações do cotidiano e em diversas áreas de estudo. Por exemplo, em geometria, podemos usar esses conceitos para calcular áreas de terrenos, de superfícies circulares e até mesmo para determinar a quantidade de material necessária para revestir uma superfície.

Além disso, em disciplinas como física e engenharia, a área e o perímetro do círculo são frequentemente utilizados para resolver problemas relacionados a movimento circular, áreas de seção transversal e muito mais.

Portanto, dominar esses conceitos não apenas nos ajuda a compreender melhor o mundo ao nosso redor, mas também nos capacita a resolver uma ampla gama de problemas de maneira eficaz e precisa.

Fique Atento: Estes conceitos, especialmente a fórmula da área do círculo, são frequentemente abordados em provas como o ENEM, exigindo que os estudantes compreendam e saibam aplicar essas fórmulas em diversos contextos matemáticos e práticos.

Contextualizando a Importância da Área do Círculo

A compreensão da área do círculo vai além da matemática pura. Ela desempenha um papel crucial em diversas áreas, como arquitetura, design, ciências naturais e até mesmo nas artes. Por exemplo, na arquitetura e no design de paisagens, o conhecimento da área do círculo é essencial para calcular espaços e distribuir elementos de forma harmoniosa. Em ciências naturais, a área do círculo pode ser aplicada no estudo de fenômenos naturais, como a análise da superfície de planetas ou a medição de corpos celestes. Até mesmo na arte, o entendimento da geometria do círculo pode inspirar e enriquecer a criação artística.

Explorando Variações e Aplicações

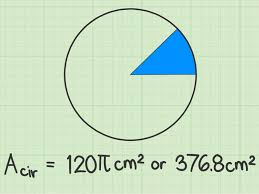
Além da área e do perímetro, os conceitos relacionados ao círculo têm várias variações e aplicações interessantes. Por exemplo, a área de um setor circular, que é uma parte do círculo limitada por dois raios e um arco, pode ser calculada usando uma fórmula específica. Da mesma forma, o comprimento de um arco de círculo, conhecido como comprimento da circunferência, pode ser calculado usando técnicas trigonométricas ou fórmulas especiais. Esses conceitos adicionais expandem ainda mais nosso entendimento da geometria circular e sua aplicabilidade em diferentes contextos.

Desafios e Oportunidades

Embora os conceitos relacionados ao círculo possam parecer simples à primeira vista, eles também apresentam desafios interessantes. Resolver problemas envolvendo círculos requer habilidades analíticas e capacidade de raciocínio abstrato. No entanto, esses desafios também representam oportunidades de crescimento e aprendizado, ajudando os estudantes a desenvolverem habilidades matemáticas essenciais, como resolução de problemas, pensamento crítico e modelagem matemática.

Portanto, o estudo da área do círculo não se limita apenas a uma fórmula matemática, mas abre portas para um mundo de descobertas, aplicações e desafios que enriquecem nossa compreensão do universo e nos capacitam a enfrentar os problemas complexos do mundo moderno.

Atenção: Esses temas, devido à sua importância e aplicabilidade em diversas áreas, podem ser abordados em questões de exames como o ENEM, exigindo dos candidatos não apenas o conhecimento teórico, mas também a capacidade de aplicar esses conceitos em diferentes contextos e resolver problemas de forma criativa e eficaz.