Simulado Aritmética e Problemas para o Enem | ENEM
SIMULADO ARITMÉTICA E PROBLEMAS PARA O ENEM
INSTRUÇÕES DO SIMULADO
OBJETIVOS
Aprimorar os conhecimentos adquiridos durante os seus estudos, de forma a avaliar a sua aprendizagem, utilizando para isso as metodologias e critérios idênticos aos maiores e melhores do País, através de simulados para , provas e questões de .
PÚBLICO ALVO DO SIMULADO
Alunos/Concursando que almejam sua aprovação no ENEM.
SOBRE AS QUESTÕES DO SIMULADO
Este simulado contém questões da ENEM que foi organizado pela bancas diversas. Estas questões são de Aritmética e Problemas, contendo os assuntos de Assuntos Diversos que foram extraídas dos anteriores ENEM, portanto este simulado contém os gabaritos oficiais.
ESTATÍSTICA DO SIMULADO
O Simulado Aritmética e Problemas para o Enem contém um total de 10 questões de com um tempo estimado de 30 minutos para sua realização. Os assuntos abordados são de Aritmética e Problemas, Assuntos Diversos para que você possa realmente simular como estão seus conhecimento no ENEM.
RANKING DO SIMULADO
Realize este simulado até o seu final e ao conclui-lo você verá as questões que errou e acertou, seus possíveis comentários e ainda poderá ver seu DESEMPENHO perante ao dos seus CONCORRENTES no ENEM. Venha participar deste Ranking e saia na frente de todos. Veja sua nota e sua colocação no RANKING e saiba se esta preparado para conseguir sua aprovação.
CARGO DO SIMULADO
Este simulado contém questões para o cargo de Aluno ENEM. Se você esta estudando para ser aprovado para Aluno ENEM não deixe de realizar este simulado e outros disponíveis no portal.
COMO REALIZAR O SIMULADO ENEM
Para realizar o simulado ENEM você deve realizar seu cadastro grátis e depois escolher as alternativas que julgar correta. No final do simulado ENEM você verá as questões que errou e acertou.
Bons Estudos! Simulado para ENEM é aqui!
- #205035
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
A contagem de bois
Em cada parada ou pouso, para jantar ou dormir, os bois são contados, tanto na chegada quanto na saída. Nesses lugares, há sempre um potreiro, ou seja, determinada área de pasto cercada de arame, ou mangueira, quando a cerca é de madeira. Na porteira de entrada do potreiro, rente à cerca, os peões formam a seringa ou funil, para afinar a fila, e então os bois vão entrando aos poucos na área cercada. Do lado interno, o condutor vai contando; em frente a ele, está o marcador, peão que marca as reses. O condutor conta 50 cabeças e grita: — Talha! O marcador, com o auxílio dos dedos das mãos, vai marcando as talhas. Cada dedo da mão direita corresponde a 1 talha, e da mão esquerda, a 5 talhas. Quando entra o último boi, o marcador diz: — Vinte e cinco talhas! E o condutor completa: — E dezoito cabeças. Isso significa 1.268 bois.
Boiada, comitivas e seus peões. In: O Estado de São Paulo, ano VI, ed. 63, 21/12/1952 (com adaptações).
Para contar os 1.268 bois de acordo com o processo descrito acima, o marcador utilizou
- a) 20 vezes todos os dedos da mão esquerda.
- b) 20 vezes todos os dedos da mão direita.
- c) todos os dedos da mão direita apenas uma vez.
- d) todos os dedos da mão esquerda apenas uma vez.
- e) 5 vezes todos os dedos da mão esquerda e 5 vezes todos os dedos da mão direita.
- #205038
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
Suponha que o universo tenha 15 bilhões de anos de idade e que toda a sua história seja distribuída ao longo de 1 ano — o calendário cósmico —, de modo que cada segundo corresponda a 475 anos reais e, assim, 24 dias do calendário cósmico equivaleriam a cerca de 1 bilhão de anos reais. Suponha, ainda, que o universo comece em 1.º de janeiro a zero hora no calendário cósmico e o tempo presente esteja em 31 de dezembro às 23 h 59 min 59,99 s. A escala abaixo traz o período em que ocorreram alguns eventos importantes nesse calendário.
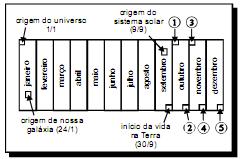

- a) 1.
- b) 2.
- c) 3.
- d) 4.
- e) 5.
- #205040
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -
Um pátio de grandes dimensões vai ser revestido por pastilhas quadradas brancas e pretas, segundo o padrão representado ao lado, que vai ser repetido em toda a extensão do pátio.
As pastilhas de cor branca custam R$ 8,00 por metro quadrado e as de cor preta, R$ 10,00. O custo por metro quadrado do revestimento será de

- a) R$ 8,20.
- b) R$ 8,40.
- c) R$ 8,60.
- d) R$ 8,80.
- e) R$ 9,00.
- #205043
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
Os números de identificação utilizados no cotidiano (de contas bancárias, de CPF, de Carteira de Identidade etc) usualmente possuem um dígito de verificação, normalmente representado após o hífen, como em 17326-9. Esse dígito adicional tem a finalidade de evitar erros no preenchimento ou digitação de documentos. Um dos métodos usados para gerar esse dígito utiliza os seguintes passos:
multiplica-se o último algarismo do número por 1, o penúltimo por 2, o antepenúltimo por 1, e assim por diante, sempre alternando multiplicações por 1 e por 2.
soma-se 1 a cada um dos resultados dessas multiplicações que for maior do que ou igual a 10.
somam-se os resultados obtidos .
calcula-se o resto da divisão dessa soma por 10, obtendo-se assim o dígito verificador.
O dígito de verificação fornecido pelo processo acima para o número 24685 é
- a) 1.
- b) 2.
- c) 4.
- d) 6.
- e) 8.
- #205046
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
Joana frequenta uma academia de ginástica onde faz exercícios de musculação. O programa de Joana requer que ela faça 3 séries de exercícios em 6 aparelhos diferentes, gastando 30 segundos em cada série. No aquecimento, ela caminha durante 10 minutos na esteira e descansa durante 60 segundos para começar o primeiro exercício no primeiro aparelho. Entre uma série e outra, assim como ao mudar de aparelho, Joana descansa por 60 segundos.
Suponha que, em determinado dia, Joana tenha iniciado seus exercícios às 10h30min e finalizado às 11h7min. Nesse dia e nesse tempo, Joana
- a) não poderia fazer sequer a metade dos exercícios e dispor dos períodos de descanso especificados em seu programa.
- b) poderia ter feito todos os exercícios e cumprido rigorosamente os períodos de descanso especificados em seu programa.
- c) poderia ter feito todos os exercícios, mas teria de ter deixado de cumprir um dos períodos de descanso especificados em seu programa.
- d) conseguiria fazer todos os exercícios e cumpriria todos os períodos de descanso especificados em seu programa, e ainda se permitiria uma pausa de 7 min.
- e) não poderia fazer todas as 3 séries dos exercícios especificados em seu programa; em alguma dessas séries deveria ter feito uma série a menos e não deveria ter cumprido um dos períodos de descanso.Responder
- #205051
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
A cisterna é um recipiente utilizado para armazenar água da chuva. Os principais critérios a serem observados para captação e armazenagem de água da chuva são: a demanda diária de água na propriedade; o índice médio de precipitação (chuva), por região, em cada período do ano; o tempo necessário para armazenagem; e a área de telhado necessária ou disponível para captação. Para fazer o cálculo do volume de uma cisterna, deve-se acrescentar um adicional relativo ao coeficiente de evaporação. Na dificuldade em se estabelecer um coeficiente confiável, a Empresa Brasileira de Pesquisa Agropecuária (EMBRAPA) sugere que sejam adicionados 10% ao volume calculado de água.
Desse modo, o volume, em m 3, de uma cisterna é calculado por
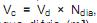
em que
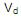
= volume de demanda da água diária (m³), Ndia = número de dias de armazenagem, e este resultado deve ser acrescido de 10%.
Para melhorar a qualidade da água, recomenda-se que a captação seja feita somente nos telhados das edificações.
Considerando que a precipitação de chuva de 1 mm sobre uma área de 1 m2 produz 1 litro de água, pode-se calcular a área de um telhado a fim de atender a necessidade de armazenagem da seguinte maneira: área do telhado (em m2 ) = volume da cisterna (em litros)/precipitação.
Disponível em: www.cnpsa.embrapa.br. Acesso em: 8 jun. 2009 (adaptado).
Para atender a uma demanda diária de 2.000 litros de água, com período de armazenagem de 15 dias e precipitação média de 110 mm, o telhado, retangular, deverá ter as dimensões mínimas de
- a) 6 metros por 5 metros, pois assim teria uma área de 30 m2 .
- b) 15 metros por 20 metros, pois assim teria uma área de 300 m2 .
- c) 50 metros por 60 metros, pois assim teria uma área de 3.000 m2 .
- d) 91 metros por 30 metros, pois assim teria uma área de 2.730 m2 .
- e) 110 metros por 30 metros, pois assim teria uma área de 3.300 m2 .
- #205052
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -
O dono de uma oficina mecânica precisa de um pistão das partes de um motor, de 68 mm de diâmetro, para o conserto de um carro. Para conseguir um, esse dono vai até um ferro velho e lá encontra pistões com diâmetros iguais a 68,21 mm; 68,102 mm; 68,001 mm; 68,02 mm e 68,012 mm.
Para colocar o pistão no motor que está sendo consertado, o dono da oficina terá de adquirir aquele que tenha o diâmetro mais próximo do que precisa.
Nessa condição, o dono da oficina deverá comprar o pistão de diâmetro
- a) 68,21 mm.
- b) 68,102 mm.
- c) 68,02 mm.
- d) 68,012 mm.
- e) 68,001 mm.
- #205053
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
O medidor de energia elétrica de uma residência, conhecido por “relógio de luz”, é constituído de quatro pequenos relógios, cujos sentidos de rotação estão indicados conforme a figura:

A medida é expressa em kWh. O número obtido na leitura é composto por 4 algarismos. Cada posição do número é formada pelo último algarismo ultrapassado pelo ponteiro.
O número obtido pela leitura em kWh, na imagem, é
- a) 2 614.
- b) 3 624.
- c) 2 715.
- d) 3 725.
- e) 4 162.
- #205054
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -
Você pode adaptar as atividades do seu dia a dia de uma forma que possa queimar mais calorias do que as gastas normalmente, conforme a relação seguinte: -
Enquanto você fala ao telefone, faça agachamentos: 100 calorias gastas em 20 minutos.
- Meia hora de supermercado: 100 calorias.
- Cuidar do jardim por 30 minutos: 200 calorias.
- Passear com o cachorro: 200 calorias em 30 minutos.
- Tirar o pó dos móveis: 150 calorias em 30 minutos.
- Lavar roupas por 30 minutos: 200 calorias.
Disponível em: http://cyberdiet.terra.com.br. Acesso em: 27 abr. 2010 (adaptado).
Uma pessoa deseja executar essas atividades, porém, ajustando o tempo para que, em cada uma, gaste igualmente 200 calorias.
A partir dos ajustes, quanto tempo a mais será necessário para realizar todas as atividades?
- a) 50 minutos.
- b) 60 minutos.
- c) 80 minutos.
- d) 120 minutos.
- e) 170 minutos.
- #205055
- Banca
- . Bancas Diversas
- Matéria
- Aritmética e Problemas
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
Observe as dicas para calcular a quantidade certa de alimentos e bebidas para as festas de fim de ano:
• Para o prato principal, estime 250 gramas de carne para cada pessoa.
• Um copo americano cheio de arroz rende o suficiente para quatro pessoas.
• Para a farofa, calcule quatro colheres de sopa por convidado.
• Uma garrafa de vinho serve seis pessoas.
• Uma garrafa de cerveja serve duas.
• Uma garrafa de espumante serve três convidados.
Quem organiza festas faz esses cálculos em cima do total de convidados, independente do gosto de cada um.
Quantidade certa de alimentos e bebidas evita o desperdício da ceia. Jornal Hoje. 17 dez. 2010 (adaptado).
Um anfitrião decidiu seguir essas dicas ao se preparar para receber 30 convidados para a ceia de Natal. Para seguir essas orientações à risca, o anfitrião deverá dispor de
- a) 120 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 15 de cerveja e 10 de espumante.
- b) 120 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 30 de cerveja e 10 de espumante.
- c) 75 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 15 de cerveja e 10 de espumante.
- d) 7,5 kg de carne, 7 copos americanos, 120 colheres de sopa de farofa, 5 garrafas de vinho, 30 de cerveja e 10 de espumante.
- e) 7,5 kg de carne, 7 copos americanos e meio de arroz, 120 colheres de sopa de farofa, 5 garrafas de vinho, 15 de cerveja e 10 de espumante.

