Prova Polícia Militar-SP - Matemática 1 - Questões e Simulados | CONCURSO

(1,0) 1 - 

Na reunião convocada pelo comandante geral, cada oficial sob seu comando teria 27 minutos para expor o seu plano de metas para o próximo semestre. Entretanto, um dos oficiais não pôde comparecer, por motivo de força maior, e, assim, cada um dos oficiais presentes teve o seu tempo de exposição aumentado para 30 minutos. O tempo total reservado pelo comandante para a exposição de seus oficiais era

(1,0) 2 - 

Os valores das parcelas mensais estabelecidas em contrato para pagamento do valor total de compra de um imóvel constituem uma PA crescente de 5 termos. Sabendo que a₁ + a₃ = 60 mil reais, e que a₁ + a₅ = 100 mil reais, pode-se afirmar que o valor total de compra desse imóvel foi, em milhares de reais, igual a

(1,0) 3 - 

O paralelogramo ABCD foi construído com a junção de dois triângulos retângulos congruentes, ABD e BCD, conforme mostra a figura.

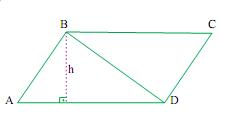
Se os lados de um triângulo medem 12 cm, 16 cm e 20 cm, então a altura indicada por h na figura mede, em centímetros, 

(1,0) 4 - 

Um determinado produto, comprado por R$ 300,00, foi vendido com um lucro correspondente a 60% do preço de venda. Sendo o lucro igual ao preço de venda menos o preço de custo, pode-se concluir que esse produto foi vendido por

(1,0) 5 - 

No final de certo jogo, Pedro tinha 30 fichas brancas, 40 pretas e 20 verdes, e João tinha 50 fichas brancas, 20 pretas e 10 verdes. Duas fichas foram retiradas aleatoriamente e simultaneamente, uma de Pedro e outra de João. A probabilidade de que a ficha retirada de Pedro seja branca, e a de João preta, é de

(1,0) 6 - 

O valor de mercado de determinado produto decresce linearmente com o tempo (t) de uso, em anos, conforme mostra o gráfico, até atingir um valor mínimo igual a 25% do valor da compra inicial, quando se estabiliza.

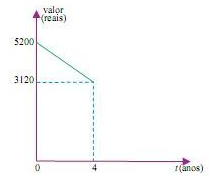
Se o valor de compra, hoje (t = 0), é de R$ 5.200,00, ele atingirá o valor mínimo daqui a

(1,0) 7 - 

Sabe-se que o ponto C pertence à reta de equação 3x + y – 4 = 0 e, também, à reta de equação x + 2y = 3. Nesse caso, é correto afirmar que o comprimento da circunferência de centro C, que tangencia o eixo x, é igual a

(1,0) 8 - 

Exposto em uma feira de ciências, um recipiente de vidro com a forma de um cilindro circular reto, cujo diâmetro da base mede 10 cm, contém água e óleo. Sabe-se que a altura do nível da água, indicada por x na figura, é igual a ²/₅ da altura do recipiente, e que o óleo ocupa a altura restante, preenchendo totalmente o recipiente.

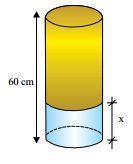
Pode-se afirmar, então, que o volume do óleo contido nesse recipiente é, em centímetros cúbicos, igual a

(1,0) 9 - 

Considere o polinômio P(x) = x⁴ + x² + bx + c, em que b e c são números inteiros. Sabe-se que P(x) é divisível por h(x) = x – 2 e que deixa resto igual a 4 quando dividido por g(x) = x + 2. Nessas condições, b e c valem, respectivamente,