Prova Enem - Matemática Enem 15 - Questões e Simulados | ENEM
📚 Simulado ENEM | Matemática e suas Tecnologias (ENEM) | cód.1530
Quer subir no ranking e garantir sua aprovação no concurso ENEM? Comece pelo simulado certo! 🥇
🎯 São milhares de simulados para concurso disponíveis para você praticar e conseguir a tão sonhada aprovação em Concurso Público.
🧪 Este Simulado ENEM foi elaborado da seguinte forma:
- 📌 Categoria: Enem
- 🏛️ Instituição: ENEM
- 👔 Cargo: . Cargos Diversos
- 📚 Matéria: Matemática e suas Tecnologias (ENEM)
- 🧩 Assuntos do Simulado:
- 🏢 Banca Organizadora: . Bancas Diversas
- ❓ Quantidade de Questões: 10
- ⏱️ Tempo do Simulado: 30 minutos
⚙️ REGRA DO SIMULADO
Este simulado é gratuito 🆓. Basta clicar no botão iniciar abaixo e preencher um breve cadastro para participar do nosso ranking.
📊 No ranking você compara sua nota com outros candidatos e acompanha sua evolução nos estudos.
🚀 Aproveite este simulado ENEM e saia na frente na sua preparação!
📖 Questões ENEM
Se ainda não estiver pronto para fazer o simulado, treine antes com nossas questões de concursos:
🎥 Vídeo Aula
Confira vídeo aulas no YouTube com foco no concurso ENEM. Estude com conteúdo gratuito e atualizado.
Assistir vídeo aula sobre ENEM
📚 Apostila
Encontre apostilas completas e materiais didáticos atualizados para o concurso ENEM.
📢 Concursos Abertos para ENEM
Veja os concursos abertos da instituição ENEM. A lista está sempre atualizada:
🍀 Boa sorte e Bons Estudos,
ConcursosAZ - Aprovando de A a Z ✅
- #22236
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 1 -
O tangram é um jogo oriental antigo, uma espécie de quebra-cabeça, constituído de sete peças: 5 triângulos retângulos e isósceles, 1 paralelogramo e 1 quadrado. Essas peças são obtidas recortando-se um quadrado de acordo com o esquema da figura 1. Utilizando-se todas as sete peças, é possível representar uma grande diversidade de formas, como as exemplificadas nas figuras 2 e 3. B
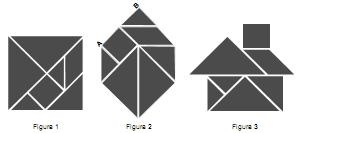
Se o lado AB do hexágono mostrado na figura 2 mede 2 cm, então a área da figura 3, que representa uma “casinha”, é igual a
- a) 4 cm2 .
- b) 8 cm2 .
- c) 12 cm2 .
- d) 14 cm2 .
- e) 16 cm2 .
- #22237
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 2 -
A figura abaixo representa o boleto de cobrança da mensalidade de uma escola, referente ao mês de junho de 2008.

Se M(x) é o valor, em reais, da mensalidade a ser paga, em que x é o número de dias em atraso, então
- a) M(x) = 500 + 0,4x.
- b) M(x) = 500 + 10x.
- c) M(x) = 510 + 0,4x.
- d) M(x) = 510 + 40x.
- e) M(x) = 500 + 10,4x.
- #22238
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 3 -

- a) carroça – semana
- b) carro – dia
- c) caminhada – hora
- d) bicicleta – minuto
- e) avião – segundo
- #22239
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 4 -
No gráfico a seguir, estão especificados a produção brasileira de café, em toneladas; a área plantada, em hectares (ha); e o rendimento médio do plantio, em kg/ha, no período de 2001 a 2008.
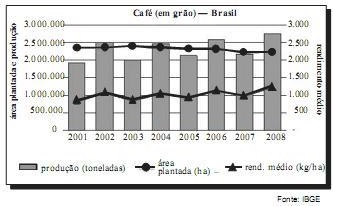
A análise dos dados mostrados no gráfico revela que
- a) a produção em 2003 foi superior a 2.100.000 toneladas de grãos.
- b) a produção brasileira foi crescente ao longo de todo o período observado.
- c) a área plantada decresceu a cada ano no período de 2001 a 2008.
- d) os aumentos na produção correspondem a aumentos no rendimento médio do plantio.
- e) a área plantada em 2007 foi maior que a de 2001.
- #22240
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 5 -
No gráfico a seguir, estão especificados a produção brasileira de café, em toneladas; a área plantada, em hectares (ha); e o rendimento médio do plantio, em kg/ha, no período de 2001 a 2008.
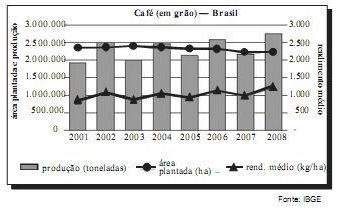
Se a tendência de rendimento observada no gráfico, no período de 2001 a 2008, for mantida nos próximos anos, então o rendimento médio do plantio do café, em 2012, será aproximadamente de
- a) 500 kg/ha.
- b) 750 kg/ha.
- c) 850 kg/ha.
- d) 950 kg/ha.
- e) 1.250 kg/ha.
- #22241
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 6 -
Fractal (do latim fractus, fração, quebrado) — objeto que pode ser dividido em partes que possuem semelhança com o objeto inicial. A geometria fractal, criada no século XX, estuda as propriedades e o comportamento dos fractais — objetos geométricos formados por repetições de padrões similares.
O triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. comece com um triângulo equilátero (figura 1);
2. construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias;
3. posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a figura 2;
4. repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (figura 3).
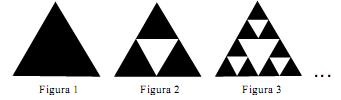
De acordo com o procedimento descrito, a figura 4 da seqüência apresentada acima é
- a)

- b)

- c)

- d)

- e)

- #22242
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 7 -

- a) a quantidade de água economizada foi de 4,5 m3 .
- b) a altura do nível da água que sobrou no reservatório, no final do dia, foi igual a 60 cm.
- c) a quantidade de água economizada seria suficiente para abastecer, no máximo, 90 casas cujo consumo diário fosse de 450 litros.
- d) os moradores dessas casas economizariam mais de R$ 200,00, se o custo de 1 m3 de água para o consumidor fosse igual a R$ 2,50.
- e) um reservatório de mesma forma e altura, mas com raio da base 10% menor que o representado, teria água suficiente para abastecer todas as casas.
- #22243
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 8 -
Suponha que o universo tenha 15 bilhões de anos de idade e que toda a sua história seja distribuída ao longo de 1 ano — o calendário cósmico —, de modo que cada segundo corresponda a 475 anos reais e, assim, 24 dias do calendário cósmico equivaleriam a cerca de 1 bilhão de anos reais. Suponha, ainda, que o universo comece em 1.º de janeiro a zero hora no calendário cósmico e o tempo presente esteja em 31 de dezembro às 23 h 59 min 59,99 s. A escala abaixo traz o período em que ocorreram alguns eventos importantes nesse calendário.
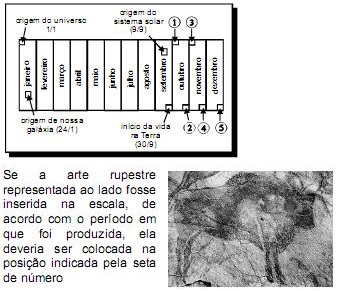
- a) 1
- b) 2
- c) 3
- d) 4
- e) 5
- #22244
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 9 -

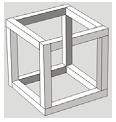
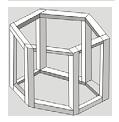
onsidere que um marceneiro tenha encontrado algumas figuras supostamente desenhadas por Escher e deseje construir uma delas com ripas rígidas de madeira que tenham o mesmo tamanho. Qual dos desenhos a seguir ele poderia reproduzir em um modelo tridimensional real?
- a)
- b)

- c)
- d)

- e)

- #22245
- Banca
- . Bancas Diversas
- Matéria
- Matemática e suas Tecnologias (ENEM)
- Concurso
- ENEM
- Tipo
- Múltipla escolha
- Comentários
- Seja o primeiro a comentar
(1,0) 10 -
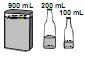
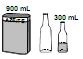
A diversidade de formas geométricas espaciais criadas pelo homem, ao mesmo tempo em que traz benefícios, causa dificuldades em algumas situações. Suponha, por exemplo, que um cozinheiro precise utilizar exatamente 100 mL de azeite de uma lata que contenha 1.200 mL e queira guardar o restante do azeite em duas garrafas, com capacidade para 500 mL e 800 mL cada, deixando cheia a garrafa maior. Considere que ele não disponha de instrumento de medida e decida resolver o problema utilizando apenas a lata e as duas garrafas. As etapas do procedimento utilizado por ele estão ilustradas nas figuras a seguir, tendo sido omitida a 5. ª etapa.
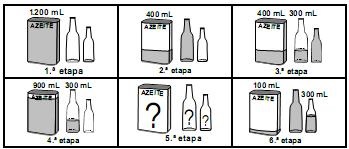
Qual das situações ilustradas a seguir corresponde à 5. ª etapa do procedimento?
- a)
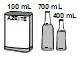
- b)
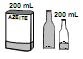
- c)
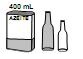
- d)
- e)